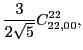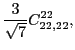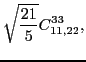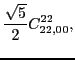next up previous
Next: Relations between the central-like Up: Effective pseudopotential for energy Previous: Time-reversal invariance and hermiticity


Relations defining the gauge-invariant pseudopotentials

As discussed in Section 2.3, when the gauge invariance is imposed on the pseudopotential, one obtains a specific set of constraints on the parameters and terms of the pseudopotential, which result from the condition of Eq. (21).

At fourth order, the gauge symmetry forces seven parameters of terms listed in the Table 4 to be specific linear combinations of the four independent ones, namely,


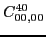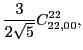$\displaystyle C_{00,00}^{40}$ $\textstyle =$ $\displaystyle \frac{3}{2\sqrt{5}}C_{22,00}^{22} ,$ (69)
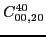$\displaystyle C_{00,20}^{40}$ $\textstyle =$ $\displaystyle \frac{3}{2\sqrt{5}}C_{22,20}^{22},$ (70)
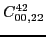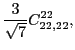$\displaystyle C_{00,22}^{42}$ $\textstyle =$ $\displaystyle \frac{3}{\sqrt{7}}C_{22,22}^{22} ,$ (71)
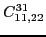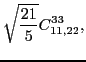$\displaystyle C_{11,22}^{31}$ $\textstyle =$ $\displaystyle \sqrt{\frac{21}{5}}C_{11,22}^{33} ,$ (72)
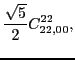$\displaystyle C_{20,00}^{20}$ $\textstyle =$ $\displaystyle \frac{\sqrt{5}}{2}C_{22,00}^{22} ,$ (73)
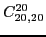$\displaystyle C_{20,20}^{20}$ $\textstyle =$ $\displaystyle \frac{\sqrt{5}}{2}C_{22,20}^{22} ,$ (74)
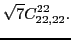$\displaystyle C_{20,22}^{22}$ $\textstyle =$ $\displaystyle \sqrt{7}C_{22,22}^{22} .$ (75)

At sixth order, imposing the gauge symmetry forces 16 terms of the pseudopotential listed in Table 5 to be specific linear combinations of 6 independent ones, namely,


$\displaystyle C_{00,00}^{60}$ $\textstyle =$ $\displaystyle \frac{1}{4\sqrt{5}}C_{22,00}^{42},$ (76)
$\displaystyle C_{00,20}^{60}$ $\textstyle =$ $\displaystyle \frac{1}{4\sqrt{5}}C_{22,20}^{42},$ (77)


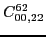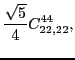$\displaystyle C_{00,22}^{62}$ $\textstyle =$ $\displaystyle \frac{\sqrt{5}}{4}C_{22,22}^{44},$ (78)
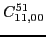$\displaystyle C_{11,00}^{51}$ $\textstyle =$ $\displaystyle \frac{9}{2} \sqrt{\frac{3}{7}}C_{33,00}^{33},$ (79)
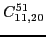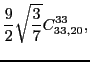$\displaystyle C_{11,20}^{51}$ $\textstyle =$ $\displaystyle \frac{9}{2} \sqrt{\frac{3}{7}}C_{33,20}^{33},$ (80)
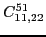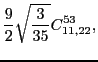$\displaystyle C_{11,22}^{51}$ $\textstyle =$ $\displaystyle \frac{9}{2} \sqrt{\frac{3}{35}}C_{11,22}^{53},$ (81)
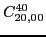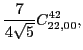$\displaystyle C_{20,00}^{40}$ $\textstyle =$ $\displaystyle \frac{7}{4 \sqrt{5}}C_{22,00}^{42} ,$ (82)
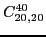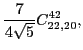$\displaystyle C_{20,20}^{40}$ $\textstyle =$ $\displaystyle \frac{7}{4 \sqrt{5}} C_{22,20}^{42},$ (83)
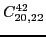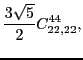$\displaystyle C_{20,22}^{42}$ $\textstyle =$ $\displaystyle \frac{3\sqrt{5}}{2}C_{22,22}^{44},$ (84)
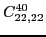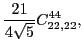$\displaystyle C_{22,22}^{40}$ $\textstyle =$ $\displaystyle \frac{21}{4\sqrt{5}}C_{22,22}^{44},$ (85)
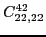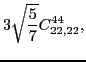$\displaystyle C_{22,22}^{42}$ $\textstyle =$ $\displaystyle 3 \sqrt{\frac{5}{7}}C_{22,22}^{44} ,$ (86)
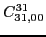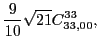$\displaystyle C_{31,00}^{31}$ $\textstyle =$ $\displaystyle \frac{9}{10}\sqrt{21}C_{33,00}^{33},$ (87)
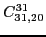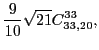$\displaystyle C_{31,20}^{31}$ $\textstyle =$ $\displaystyle \frac{9}{10}\sqrt{21}C_{33,20}^{33},$ (88)
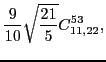$\displaystyle C_{31,22}^{31}$ $\textstyle =$ $\displaystyle \frac{9}{10}\sqrt{\frac{21}{5}}C_{11,22}^{53},$ (89)
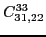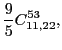$\displaystyle C_{31,22}^{33}$ $\textstyle =$ $\displaystyle \frac{9}{5}C_{11,22}^{53},$ (90)
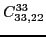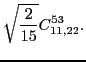$\displaystyle C_{33,22}^{33}$ $\textstyle =$ $\displaystyle \sqrt{\frac{2}{15}}C_{11,22}^{53}.$ (91)

next up previous
Next: Relations between the central-like Up: Effective pseudopotential for energy Previous: Time-reversal invariance and hermiticity
Jacek Dobaczewski 2011-03-20