


Next: Relations defining the gauge-invariant
Up: Effective pseudopotential for energy
Previous: Conclusions
Time-reversal invariance and hermiticity of the pseudopotential
The pseudopotential studied in this work is a contact interaction
built with derivative and spin operators. Furthermore, the choice
concerning the formalism is the use of the spherical tensors. Under
these assumptions, the general structure of the pseudopotential is
based on the following building blocks,
![\begin{displaymath}
\hat{V}_0 =
\left[ \left[K'_{\tilde{n}'\tilde{L}'} K_{\tilde...
...]_{0} \hat{\delta}_{12}(\bm{r}'_1\bm{r}'_2;\bm{r}_1\bm{r}_2)
.
\end{displaymath}](img511.png) |
(55) |
The final coupling to a scalar ensures that  is invariant
under space rotation Moreover, provided that
is invariant
under space rotation Moreover, provided that
 is even, it is also invariant under space-inversion. Now we proceed
to explore another fundamental symmetry, the time-reversal, and later
we also require the hermiticity of the pseudopotential.
is even, it is also invariant under space-inversion. Now we proceed
to explore another fundamental symmetry, the time-reversal, and later
we also require the hermiticity of the pseudopotential.
The time-reversal operator
 , where
, where
 is the complex conjugation in space representation, can be
explicitly applied to the spherical-tensor representations of
momentum and spin operators, Eqs. (3), (5), and
(6), which gives the generic result for spherical tensors,
is the complex conjugation in space representation, can be
explicitly applied to the spherical-tensor representations of
momentum and spin operators, Eqs. (3), (5), and
(6), which gives the generic result for spherical tensors,
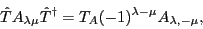 |
(56) |
where  are numerical phase factors. In our case, we obtain
are numerical phase factors. In our case, we obtain  for the momentum operator and
for the momentum operator and
 for the scalar (
for the scalar ( )
and vector (
)
and vector ( ) spin operators. Moreover, since the Clebsh-Gordan coefficients
are real, rule (56) propagates through the angular
momentum coupling, that is, if phase factors
) spin operators. Moreover, since the Clebsh-Gordan coefficients
are real, rule (56) propagates through the angular
momentum coupling, that is, if phase factors  and
and  characterize tensors
characterize tensors  and
and  , respectively,
then the coupled tensor,
, respectively,
then the coupled tensor,
![\begin{displaymath}
A''_{\lambda''\mu''} = [A_\lambda A'_{\lambda'}]_{\lambda''\...
...''}_{\lambda\mu\lambda'\mu'}
A_{\lambda\mu}A'_{\lambda'\mu'},
\end{displaymath}](img525.png) |
(57) |
is characterized by the product of phase factors
 (cf. Appendix B in Ref. [2]).
Therefore, the coupled operators appearing in
(cf. Appendix B in Ref. [2]).
Therefore, the coupled operators appearing in  (55) are
characterized by the following values of phase factors,
(55) are
characterized by the following values of phase factors,
Finally, because the Dirac delta is real, for  we have,
we have,
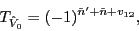 |
(61) |
and by taking into account the space-inversion invariance, it boils down to
 |
(62) |
This justifies the phase factor  in the
definition of the pseudopotential in Eq. (2), which ensures that
for real parameters, all terms of the pseudopotential are time-even.
in the
definition of the pseudopotential in Eq. (2), which ensures that
for real parameters, all terms of the pseudopotential are time-even.
Now we can proceed to calculate the adjoint
of the operator
 (55) multiplied by the phase factor derived
above, that is,
(55) multiplied by the phase factor derived
above, that is,
![\begin{displaymath}
\left(i^{v_{12}}\hat{V}_0\right)^\dagger = (-i)^{v_{12}}
\le...
...t]_{0} \hat{\delta}_{12}(\bm{r}'_1\bm{r}'_2;\bm{r}_1\bm{r}_2),
\end{displaymath}](img536.png) |
(63) |
where we treat the space derivatives of the Dirac delta like ordinary
numbers and the space variables had to be exchanged,
 and
and
 .
.
Properties of generic spherical tensors under the complex
and Hermitian conjugations are given by the following rules,
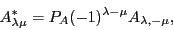 |
(64) |
 |
(65) |
where the phase factors  and
and  can be directly derived from
definitions (3), (5), and (6), that
is,
can be directly derived from
definitions (3), (5), and (6), that
is,  and
and
 . These rules also propagate
through the angular
momentum coupling, that is,
. These rules also propagate
through the angular
momentum coupling, that is,
 and, for commuting
operators, which is the case here,
and, for commuting
operators, which is the case here,
 .
Therefore, we have,
.
Therefore, we have,
![\begin{displaymath}
P_{\left[K_{\tilde{n}'\tilde{L}'} K'_{\tilde{n}\tilde{L}}\right]_{S}}
=(-1)^{\tilde{n}'+\tilde{n}}=+1 ,
\end{displaymath}](img547.png) |
(66) |
and
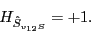 |
(67) |
Finally, the adjoint operator of Eq. (63) is given by
![\begin{displaymath}
\left(i^{v_{12}}\hat{V}_0\right)^\dagger = (-i)^{v_{12}}
\le...
...t]_{0} \hat{\delta}_{12}(\bm{r}'_1\bm{r}'_2;\bm{r}_1\bm{r}_2),
\end{displaymath}](img536.png) |
(68) |
where the last equality results from flipping the order of coupling of the
operators
 and
and
 ,
which brings out the phase factor of
,
which brings out the phase factor of
 .
Therefore, the time-even tensor
.
Therefore, the time-even tensor
 is not self-adjoint,
but we can hermitize it by using the expression given in Eq. (2).
is not self-adjoint,
but we can hermitize it by using the expression given in Eq. (2).



Next: Relations defining the gauge-invariant
Up: Effective pseudopotential for energy
Previous: Conclusions
Jacek Dobaczewski
2011-03-20
![]() is invariant
under space rotation Moreover, provided that
is invariant
under space rotation Moreover, provided that
![]() is even, it is also invariant under space-inversion. Now we proceed
to explore another fundamental symmetry, the time-reversal, and later
we also require the hermiticity of the pseudopotential.
is even, it is also invariant under space-inversion. Now we proceed
to explore another fundamental symmetry, the time-reversal, and later
we also require the hermiticity of the pseudopotential.
![]() , where
, where
![]() is the complex conjugation in space representation, can be
explicitly applied to the spherical-tensor representations of
momentum and spin operators, Eqs. (3), (5), and
(6), which gives the generic result for spherical tensors,
is the complex conjugation in space representation, can be
explicitly applied to the spherical-tensor representations of
momentum and spin operators, Eqs. (3), (5), and
(6), which gives the generic result for spherical tensors,
![]() (55) multiplied by the phase factor derived
above, that is,
(55) multiplied by the phase factor derived
above, that is,