


Next: Wave functions
Up: Single-particle wave functions and
Previous: Single-particle wave functions and
Analytical results
Following Ref. [48], we express solutions of the radial Schrödinger equation
with the PTG potential (1) as functions of the variable x:
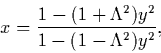 |
(20) |
where y is a function of the radial coordinate R, given by
Eqs. (4) and (5).
In the variable x, the Schrödinger equation transforms into
the Jacobi equation, and its general solution
can be expressed by means of the hypergeometric function:
| |
|
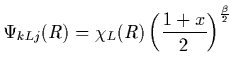 |
(21) |
| |
|
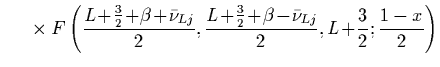 |
|
where
![\begin{displaymath}
\chi_L(R)={s^{1\over2}\over R}
\bigl[ 1 + \Lambda^2-(1-\Lamb...
...)\bigl]^{1\over4}
\biggl({1-x\over2}\biggr)^{ L+ 1 \over 2 } .
\end{displaymath}](img55.gif) |
(22) |
For a given complex momentum k,
the wave function is specified by two dimensionless parameters:
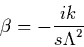 |
(23) |
and
![\begin{displaymath}\bar\nu_{Lj} = \biggl[\bigl(\nu_{Lj}+{1\over2}\bigr)^2
+\beta^2\bigl(1-\Lambda^2\bigr)
\biggr]^{1\over2} .
\end{displaymath}](img57.gif) |
(24) |
The bound states occur for parameters  defined by:
defined by:
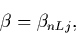 |
(25) |
where
and  .
In this case, the hypergeometric function reduces to the Jacobi polynomial,
and the solution reads [48]:
.
In this case, the hypergeometric function reduces to the Jacobi polynomial,
and the solution reads [48]:
| |
|
![$\displaystyle \Psi_{nLj} = {\cal N}_{nLj}
\bigl[1+\Lambda^2-(1-\Lambda^2)x\bigr]^{1\over4}$](img65.gif) |
|
| |
|
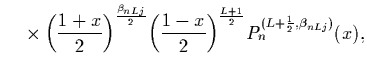 |
(27) |
where
 is a normalization factor, and the number of
bound states is limited by condition
is a normalization factor, and the number of
bound states is limited by condition
 ,
which ensures that the eigenfunctions vanish
at the infinity.
,
which ensures that the eigenfunctions vanish
at the infinity.
The bound-state energies are given by
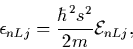 |
(28) |
where the dimensionless eigenenergies are
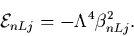 |
(29) |
It can be seen from the above equation
that the tail of a bound-state wave functions for
 ,
,
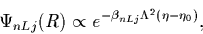 |
(30) |
does not explicitly depend on L, i.e., there
is no influence of centrifugal barrier on any partial wave.
If
 ,
the resonances will occur for integer n such that:
,
the resonances will occur for integer n such that:
![\begin{displaymath}
n > \frac{1}{2}\bigl[ \Lambda ({\Lambda}^2-2)^{-1/2}(\nu_{Lj} + \frac{1}{2})-1
\bigr]
\end{displaymath}](img73.gif) |
(31) |
The dimensionless resonance energy is then:
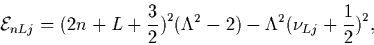 |
(32) |
and the dimensionless resonance width is:
In the limit:
 ,
the resonance width is:
,
the resonance width is:
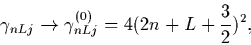 |
(34) |
and, hence, the ratio:
 ,
for all values of parameter
,
for all values of parameter 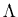 .
For small
.
For small
 ,
we have:
,
we have:
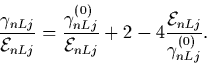 |
(35) |
This ratio depends strongly on 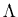 .
For large (n,L), the quantities
.
For large (n,L), the quantities
 and
and
 are proportional to
(2n+L)2 and their ratio is:
are proportional to
(2n+L)2 and their ratio is:
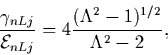 |
(36) |
i.e.
 for
for
 .
Therefore, in our numerical
examples we present results for
.
Therefore, in our numerical
examples we present results for 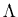 =3 and 7, which are
the values on two sides of the limiting case defined by the widths
of resonances being equal to resonance energies.
=3 and 7, which are
the values on two sides of the limiting case defined by the widths
of resonances being equal to resonance energies.
Solutions in the continuum can be found by analytically continuing
the eigenfunctions from a discrete negative energy to positive
continuous energy (see Eq. (21)). The solutions obtained in this
way are proportional to hypergeometric functions. Imposing the
boundary condition that an incoming wave has the momentum k, one
can determine the scattering function for each angular
momentum [48]. Using the asymptotic behavior of the most general
solution (21) one obtains the matrix elements of the
S-matrix:
Expression (37) yields the matrix elements of S-matrix
for the Schrödinger problem with the PTG potential without any
restrictions, i.e., (37) contains informations about
all mathematical solutions, both physical and unphysical ones. The
poles of the S-matrix in the variable
 ,
correspond to the remarkable solutions [65] depending
on the asymptotic behavior of solutions.
,
correspond to the remarkable solutions [65] depending
on the asymptotic behavior of solutions.



Next: Wave functions
Up: Single-particle wave functions and
Previous: Single-particle wave functions and
Jacek Dobaczewski
1999-05-16
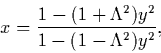
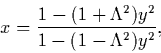
![\begin{displaymath}\bar\nu_{Lj} = \biggl[\bigl(\nu_{Lj}+{1\over2}\bigr)^2
+\beta^2\bigl(1-\Lambda^2\bigr)
\biggr]^{1\over2} .
\end{displaymath}](img57.gif)

![$\displaystyle +\Lambda^2 \bigl(\nu_{Lj}+{1\over2}\bigr)^2
\biggr)\biggr]^{1\over2}
- \biggl(2n+L+{3\over2}\biggr)$](img63.gif)
![]() ,
,
![]() ,
the resonances will occur for integer n such that:
,
the resonances will occur for integer n such that:
![]() ,
correspond to the remarkable solutions [65] depending
on the asymptotic behavior of solutions.
,
correspond to the remarkable solutions [65] depending
on the asymptotic behavior of solutions.