


Next: Figures
Up: Continuum effects for the
Previous: Bibliography
Tables
Table 1:
Parameters used to draw the potentials
presented in Fig. 1. Parameters
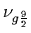 and
and
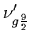 are used with the PTG and
PTG' centrifugal barriers, respectively.
are used with the PTG and
PTG' centrifugal barriers, respectively.
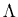 |
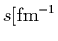 |
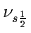 |
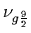 |
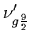 |
| 1 |
0.2192 |
6.719 |
6.188 |
7.199 |
| 3 |
0.09259 |
5.165 |
5.470 |
5.176 |
| 7 |
0.04059 |
5.034 |
5.372 |
4.693 |
Table 2:
Depth parameters of the PTG potential, for which the
3s1/2 state is resonant, virtual, or bound, and for which the
2d3/2 state is resonant or virtual. The other two
parameters are 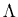 =7 and s=0.04059.
=7 and s=0.04059.
| case |
|
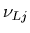 |
energy |
| (a) |
resonant 3s1/2 state |
4.882 |
 =(74-4225i)keV =(74-4225i)keV |
| (b) |
virtual 3s1/2 state |
4.972 |
 =-84keV =-84keV |
| (c) |
bound 3s1/2 state |
5.034 |
 =-74keV =-74keV |
| (d) |
resonant 2d3/2 state |
4.850 |
 =(649-2610i)keV =(649-2610i)keV |
| (c) |
virtual 2d3/2 state |
4.900 |
 =(-247-1776i)keV =(-247-1776i)keV |
Table 3:
Depth parameters of the PTG' potential (9)
defining the neutron spectrum used in the HFB calculations.
Parameters not given here are listed in Table 2.
| Lj |
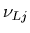 |
Lj |
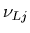 |
Lj |
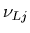 |
Lj |
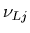 |
| s 1/2 |
Table 2 |
p 1/2 |
4.640 |
p 3/2 |
4.880 |
d 3/2 |
Table 2 |
| d 5/2 |
5.180 |
f 5/2 |
4.300 |
f 7/2 |
4.720 |
g 7/2 |
4.420 |
| g 9/2 |
4.800 |
h 9/2 |
4.493 |
h11/2 |
4.992 |
i11/2 |
4.493 |
| i13/2 |
4.493 |
j13/2 |
4.493 |
|
|
|
|
Table 4:
Properties of the HFB solutions obtained for the
PTG' potentials which give the
resonant (a), virtual (b), and weakly bound (c) 3s1/2single-particle states, or the 2d3/2low-energy narrow resonances at two different positions.
The neutron Fermi energies 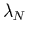 and average pairing gaps
and average pairing gaps
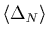 [6] are given together
with the canonical energies
[6] are given together
with the canonical energies
 [12] and occupation factors
[12] and occupation factors
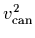 .
All energies are in keV.
.
All energies are in keV.
| case |
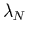 |
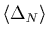 |
Lj |
 |
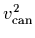 |
| (a) |
-314 |
1146 |
3s1/2 |
2148 |
0.0321 |
| (b) |
-384 |
1292 |
|
1043 |
0.1002 |
| (c) |
-488 |
1421 |
|
390 |
0.2083 |
| (d) |
-436 |
1217 |
2d3/2 |
1765 |
0.0548 |
| (c) |
-488 |
1421 |
|
1107 |
0.1149 |



Next: Figures
Up: Continuum effects for the
Previous: Bibliography
Jacek Dobaczewski
1999-05-16