Results

We begin our discussion from Fig. 1, which shows the quadrupole GOA inertia $B_{20}$ (8) for $^{258}$Fm calculated along the aEF path in the SkM$^*$+seniority model. The corresponding proton and neutron contributions are also depicted; they are related to the total inertia through Eqs. (10) and (11).

Figure 1: The total (t) GOA quadrupole collective inertia and its proton (p) and neutron (n) components calculated for $^{258}$Fm in the SkM$^*$ model with seniority pairing along the asymmetric elongated static path to fission.

The behavior of the total inertia can easily be traced back to the proton and neutron shell effects that are responsible for characteristic fluctuations in the collective mass.

Figure 2: Comparison of $B_{20}$ in GOA and CRA for $^{252}Fm$ calculated along the symmetric compact path to fission in Skyrme-HF (SLy4+DDDI) and Gogny-HF (D1S) models.

Figure 2 compares the values obtained in SLy4+DDDI and D1S models for $^{252}$Fm along the sCF static fission path. While the SLy4 values usually exceed those obtained with the Gogny force by more than a factor of two, the general patterns of $B_{20}(Q_{20})$ are fairly similar. The same conclusion holds for comparison between GOA and cranking inertia, with the cranking value being larger. A very interesting feature of the self-consistent inertia parameters is their regular behavior at large elongations. This has not been seen in earlier calculations using phenomenological potentials (see, e.g., Ref.[14]), where the oscillating behavior of $B_{20}$ persisted in the whole deformation range.

Figure 3: The zero-point energy correction (12) in GOA along the aEF fission path in $^{252}$Fm calculated in SLy4-DDDI (+) and D1S (X) models.

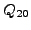
In order to calculate the collective potential $V(q)$ and fission barriers, the zero-point energy has to be evaluated first. The ZPE correction (12) for $^{252}$Fm calculated in SLy4+DDDI and D1S is shown in Fig. 3. One sees a qualitative and quantitative agreement between both variants of calculation. The largest correction is predicted around the first minimum ($Q_{20}$$\approx$25 b). As seen in Fig. 4, the inner and outer fission barriers in $^{252}$Fm are significantly modified by the ZPE correction. Namely, the barriers calculated with the corrected collective potential are $\sim$1MeV higher in the whole range of $Q_{20}$.

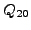Figure 4: The collective potential in $^{252}$Fm in SLy4-DDDI along the aEF fission path without ($E^{\rm tot}$; thin line) and with ( $E^{\rm tot}_{\rm cor}-E_0$; thick line) the ZPE correction included.

Finally, Figs. 5 and 6 display the collective potentials and inertia parameters (in GOA and CRA) in $^{256}$Fm and $^{258}$Fm, respectively, calculated along the symmetric (sEF and sCF) and asymmetric (aEF) fission paths[13].

Figure 5: The collective potential (left-hand scale) and corresponding GOA and CRA quadrupole inertia (right-hand scale) along three fission paths in $^{256}$Fm using the SkM$^*$+seniority model.

Figure 6: Similar to Fig. 5 except for $^{258}$Fm.

These results confirm the previous observations; namely, the deformation patterns of collective inertia in CRA and GOA are very similar, with the cranking values being appreciably higher.