Inertia Tensor and Zero-Point Energy

In order to calculate the inertia tensor one usually applies the GOA or uses the cranking model formalism. In both cases, the main task is the calculation of mass tensors $\bm M^{(k)}$,

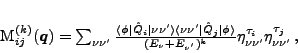$$M^{(k)}_{ij}(\bm q) = \sum_{\nu\nu'} \frac{\langle\phi\v... ...}\eta^{\tau_i}_{\nu\nu^\prime}\eta^{\tau_j}_{\nu\nu^\prime}\,,$$ (7)

where $q_i=\langle \hat Q_i\rangle$ are the collective coordinates ($i$ stands for $\lambda\mu$), $\vert\nu\nu^\prime\rangle = \alpha^\dagger_\nu\alpha^\dagger_{\nu^\prime}\vert\phi\rangle$ is a two-quasiparticle state, and $E_\nu$ is the quasiparticle energy, and $\eta^{\tau_i}_{\nu\nu'}=u_\nu v_{\nu'}+\tau_i u_\nu v_{\nu'}$. Factors $u_\nu$ and $v_\nu$ are the BCS amplitudes and the phase $\tau_i$ depends on the assumed definition of $\hat Q_i$.

Both in the GOA and cranking, the inertia tensor can be given by compact expressions[3,4]

$$\bm B^{\rm GOA} = 2\bm\Sigma^{(2)}[\bm\Sigma^{(1)}]^{-1}\bm\Sigma^{(2)}\,,$$ (8)

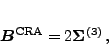$$\bm B^{\rm CRA} = 2\bm\Sigma^{(3)}\,,$$ (9)

where matrices $\bm\Sigma^{(k)}$ read

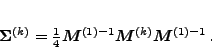$$\bm\Sigma^{(k)}=\frac{1}{4}\bm M^{(1)-1}\bm M^{(k)}\bm M^{(1)-1}\,.$$ (10)

In the nuclear case two kinds of fermions are present. The total covariant inverse inertia for a composite system is given as a sum of proton and neutron covariant inertia tensors [3]. This leads to the final expression

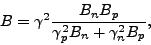$$B = \gamma^2\frac{B_n B_p} {\gamma^2_p B_n + \gamma^2_n B_p},$$ (11)

where $\gamma$ is the total metric tensor, which is a sum of proton ($\gamma_p$) and neutron ($\gamma_n$) contributions.

We conclude this section by recalling that the zero-point energy in the GOA can also be expressed through quantities (10)[4], i.e.,

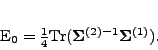$$E_0=\frac{1}{4}\mbox{Tr}(\bm\Sigma^{(2)-1}\bm\Sigma^{(1)}).$$ (12)