


Next: Local gauge invariance
Up: Local Density Approximation for
Previous: The symmetry
The Energy Density Functional
In the HFB theory the expectation value of Hamiltonian in state
 is a functional of the density matrices, and reads
is a functional of the density matrices, and reads
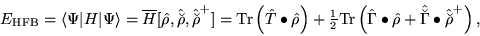 |
(72) |
where  denotes integration over spatial coordinates and
summation over spin and isospin indices.
Nuclear many-body Hamiltonian
denotes integration over spatial coordinates and
summation over spin and isospin indices.
Nuclear many-body Hamiltonian  ,
,
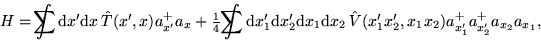 |
(73) |
is composed of one-body kinetic energy  and two-body
interaction
and two-body
interaction  , being expressed in (73) by
matrix
, being expressed in (73) by
matrix  and the
antisymmetrized matrix elements
and the
antisymmetrized matrix elements
 , respectively.
Matrices
, respectively.
Matrices  and
and
 are the
single-particle (p-h) and pairing (p-p) self-consistent potentials,
respectively,
are the
single-particle (p-h) and pairing (p-p) self-consistent potentials,
respectively,
where  =
=
 and
and



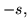
 . In Eqs. (74) and (75) we have indicated that the
p-h and p-p potentials can be determined by different two-body interactions,
. In Eqs. (74) and (75) we have indicated that the
p-h and p-p potentials can be determined by different two-body interactions,
 and
and
 , called effective interactions in the
p-h and the p-p channel, respectively. This
places further derivations in the framework of the energy-density
formalism that is not based on a definite Hamiltonian
(73). Moreover, effective interactions,
, called effective interactions in the
p-h and the p-p channel, respectively. This
places further derivations in the framework of the energy-density
formalism that is not based on a definite Hamiltonian
(73). Moreover, effective interactions,
 and
and
 , are supposed to
be, in general, density-dependent.
, are supposed to
be, in general, density-dependent.
In the case of the Skyrme effective interaction, as well as
in the framework of the LDA, the energy functional of Eq. (72) is a three-dimensional spatial integral,
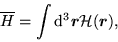 |
(76) |
of local energy density
 that is a real, scalar,
time-even, and isoscalar function of local densities and their first
and second derivatives. (Isospin-breaking terms, like those
resulting from different neutron and proton masses and from the
Coulomb interaction, can be easily added and, for simplicity, are not
considered in the present study.) In the case of no proton-neutron
mixing, the construction of the most general energy density
that is quadratic in one-body local densities was
presented in detail in Ref. [173]. With the proton-neutron
mixing included, the construction can be performed analogically by
including the additional non-zero local densities derived in Sec. 3. Then the energy density can be written in the following
form:
that is a real, scalar,
time-even, and isoscalar function of local densities and their first
and second derivatives. (Isospin-breaking terms, like those
resulting from different neutron and proton masses and from the
Coulomb interaction, can be easily added and, for simplicity, are not
considered in the present study.) In the case of no proton-neutron
mixing, the construction of the most general energy density
that is quadratic in one-body local densities was
presented in detail in Ref. [173]. With the proton-neutron
mixing included, the construction can be performed analogically by
including the additional non-zero local densities derived in Sec. 3. Then the energy density can be written in the following
form:
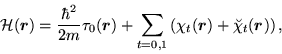 |
(77) |
where we assumed that the neutron and proton masses are equal.
The p-h and p-p interaction energy densities,
 and
and
 , for
, for  =0 depend quadratically on the isoscalar
densities, and for
=0 depend quadratically on the isoscalar
densities, and for  =1 - on the isovector ones. Based on general rules
of constructing the energy density, Sec. 3.3, one obtains
=1 - on the isovector ones. Based on general rules
of constructing the energy density, Sec. 3.3, one obtains
where  stands for the vector product, and
stands for the vector product, and
In Eqs. (78) and (80) squares always denote
total lengths in space and/or iso-space, for complex densities taken
in the complex sense, e.g.,
 . In the p-p energy
density (80) we show only terms in which the products of
real parts are added to products of imaginary parts. According to the
rules based on the
. In the p-p energy
density (80) we show only terms in which the products of
real parts are added to products of imaginary parts. According to the
rules based on the  -symmetry, Sec. 3.3, similar terms
with both products subtracted from one another are also allowed. We
do not show them explicitly, because they have exactly the form of
Eq. (80), but without complex conjugations and with
absolute values replaced by real parts of products.
-symmetry, Sec. 3.3, similar terms
with both products subtracted from one another are also allowed. We
do not show them explicitly, because they have exactly the form of
Eq. (80), but without complex conjugations and with
absolute values replaced by real parts of products.
When the effective interaction is density-dependent all coupling
constants,  's and
's and  's, may also depend on density. If
this is the case, however, terms that can be transformed into one
another by integration by parts are not anymore equivalent. Then,
five more types of terms may appear in the energy density, see Ref. [173]; we do not consider such a possibility in the present
study.
Note that in the p-h channel all coupling constants appear in two
flavors, for
's, may also depend on density. If
this is the case, however, terms that can be transformed into one
another by integration by parts are not anymore equivalent. Then,
five more types of terms may appear in the energy density, see Ref. [173]; we do not consider such a possibility in the present
study.
Note that in the p-h channel all coupling constants appear in two
flavors, for  =0 and 1, while in the p-p channel each one appears
exclusively either for
=0 and 1, while in the p-p channel each one appears
exclusively either for  =0, or for
=0, or for  =1.
=1.
The expression (77) is fairly general. In particular, it
is not based on any particular two-body interaction. However,
if one assumes that
the underlying two-body potential is local and momentum-independent,
the form of (77) can be simplified and the
number of coupling constants can be reduced. Two particular cases
of practical interest
are discussed in the following.
Subsections



Next: Local gauge invariance
Up: Local Density Approximation for
Previous: The symmetry
Jacek Dobaczewski
2004-01-03
![]() is a functional of the density matrices, and reads
is a functional of the density matrices, and reads
![]() and
and
![]() , for
, for ![]() =0 depend quadratically on the isoscalar
densities, and for
=0 depend quadratically on the isoscalar
densities, and for ![]() =1 - on the isovector ones. Based on general rules
of constructing the energy density, Sec. 3.3, one obtains
=1 - on the isovector ones. Based on general rules
of constructing the energy density, Sec. 3.3, one obtains
![]() 's and
's and ![]() 's, may also depend on density. If
this is the case, however, terms that can be transformed into one
another by integration by parts are not anymore equivalent. Then,
five more types of terms may appear in the energy density, see Ref. [173]; we do not consider such a possibility in the present
study.
Note that in the p-h channel all coupling constants appear in two
flavors, for
's, may also depend on density. If
this is the case, however, terms that can be transformed into one
another by integration by parts are not anymore equivalent. Then,
five more types of terms may appear in the energy density, see Ref. [173]; we do not consider such a possibility in the present
study.
Note that in the p-h channel all coupling constants appear in two
flavors, for ![]() =0 and 1, while in the p-p channel each one appears
exclusively either for
=0 and 1, while in the p-p channel each one appears
exclusively either for ![]() =0, or for
=0, or for ![]() =1.
=1.