Building blocks

We begin by recalling definitions that are used to construct operators and densities in the spin and position space. The basic building blocks are given as in Eqs. (8)-(9) of [4], i.e.,

$$\sigma_{v=0,0} = \sigma_0 ,$$ (14)

$$\sigma_{v=1,\mu=\left\{-1,0,1\right\}} = -i \left\{{\textstyle{\frac{ 1}{\sqrt{2}}}}\left(\sigma_{ x} -i\... ...extstyle{\frac{-1}{\sqrt{2}}}}\left(\sigma_{ x} +i\sigma_{ y}\right)\right\} ,$$ (15)

$$\nabla_{1,\mu=\left\{-1,0,1\right\}} = -i \left\{{\textstyle{\frac{ 1}{\sqrt{2}}}}\left(\nabla_x-i\nabla... ...la_z, {\textstyle{\frac{-1}{\sqrt{2}}}}\left(\nabla_x+i\nabla_y\right)\right\}$$ (16)

$$k_{1,\mu=\left\{-1,0,1\right\}} = -i \left\{{\textstyle{\frac{ 1}{\sqrt{2}}}}\left(k_x-ik_y\right), k_z, {\textstyle{\frac{-1}{\sqrt{2}}}}\left(k_x+ik_y\right)\right\} ,$$ (17)

where $\vec{k}$ is the relative momentum operator:

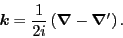$$\vec{k}=\frac{1}{2i}\left(\vec{\nabla}-\vec{\nabla}'\right).$$ (18)

All possible N$^3$LO differential operators $D_{nLM}$, which can be built of gradients (16), are given in the Table I of Ref. [4], where $n$ is the order of the operator and $L$ is its rank with magnetic projection $M$. Exactly in the same way, in Ref. [4] we defined the operators $K_{nLM}$, which are spherical tensors built of the relative momentum operators $k$ (17).

Hermitian-conjugation properties of the building blocks read:

$$\sigma_{v\mu}^+ = Q_\sigma(-1)^{v-\mu}\sigma_{v,-\mu} \quad\mbox{for}\quad Q_\sigma=+1,$$ (19)

$$\nabla_{1\mu}^+ = Q_\nabla(-1)^{1-\mu}\nabla_{1,-\mu} \quad\mbox{for}\quad Q_\nabla=-1,$$ (20)

$$k_{1\mu}^+ = Q_k (-1)^{1-\mu} k_{1,-\mu} \quad\mbox{for}\quad Q_k =+1.$$ (21)

For any pair of commuting operators $A_{\lambda\mu}$ and $B_{\lambda\mu}$ that have the following hermitian-conjugation properties:

$$A^+_{\lambda\mu} = Q_A(-1)^{\lambda-\mu} A_{\lambda,-\mu} ,$$ (22)

$$B^+_{\lambda'\mu'} = Q_B(-1)^{\lambda'-\mu'}B_{\lambda',-\mu'},$$ (23)

the operator $C_{LM}$ built by the angular momentum coupling,

$$C_{LM} \equiv [A_\lambda B_{\lambda'}]_{LM} = \sum_{\mu\mu'} C^{LM}_{\lambda\mu\lambda'\mu'} A_{\lambda\mu}B_{\lambda'\mu'} ,$$ (24)

behaves under the hermitian conjugation as:

$$C^+_{LM} = Q_C(-1)^{L-M} C_{L,-M} \quad\mbox{for}\quad Q_C=Q_AQ_B .$$ (25)

As a consequence, we have

$$D^+_{nLM} = (-1)^{n} (-1)^{L-M}D_{nL,-M} ,$$ (26)

$$K^+_{nLM} = (-1)^{L-M}K_{nL,-M} .$$ (27)

We note that the gradient operators (16) and (17) obey the Biedenharn-Rose phase conventions of

$$\nabla_{1\mu}^* = (-1)^{1-\mu}\nabla_{1,-\mu} ,$$ (28)

$$k_{1\mu}^* = - (-1)^{1-\mu} k_{1,-\mu} ,$$ (29)

which gives

$$D^*_{nLM} = (-1)^{L-M}D_{nL,-M} ,$$ (30)

$$D^+_{nLM} = (-1)^{n}D^*_{nLM} ,$$ (31)

$$D^T_{nLM} = (-1)^{n}D_{nLM} ,$$ (32)

and

$$K^*_{nLM} = (-1)^{n}(-1)^{L-M}K_{nL,-M},$$ (33)

$$K^+_{nLM} = (-1)^{n}K^*_{nLM} ,$$ (34)

$$K^T_{nLM} = (-1)^{n}K_{nLM} ,$$ (35)

where superscript $T$ denotes the transposed operator.