Second order

At second order, we obtain the same restrictions of the EDF as those already identified for the Skyrme functional, see Ref. [24] for a complete list thereof. Then, 5 dependent coupling constants are equal to specific linear combinations of 4 independent ones:

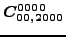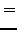$$\bm{C_{00,2000}^{0000}} = -{}{C_{00,1101}^{1101}} ,$$ (114)

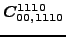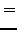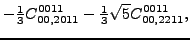$$\bm{C_{00,1110}^{1110}} = -\tfrac{1}{3}{}{C_{00,2011}^{0011}}-\tfrac{1}{3} \sqrt{5} {}{C_{00,2211}^{0011}} ,$$ (115)

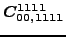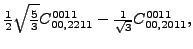$$\bm{C_{00,1111}^{1111}} = \tfrac{1}{2} \sqrt{\tfrac{5}{3}} {}{C_{00,2211}^{0011}}-\tfrac{1}{\sqrt{3}}{}{C_{00,2011}^{0011}} ,$$ (116)

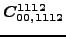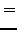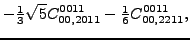$$\bm{C_{00,1112}^{1112}} = -\tfrac{1}{3} \sqrt{5} {}{C_{00,2011}^{0011}}-\tfrac{1}{6}{}{C_{00,2211}^{0011}} ,$$ (117)

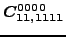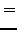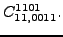$$\bm{C_{11,1111}^{0000}} = {}{C_{11,0011}^{1101}} .$$ (118)

These relations are obtained by imposing either Galilean or gauge invariance. In Eqs. (114)-(118), coupling constants corresponding to terms that depend on time-even densities are marked by using the bold-face font. The same convention also applies below.

At this order, the Galilean or gauge invariant energy density of Eq. (43) is composed of three terms corresponding to unrestricted coupling constants:

$${}{G_{20,0000}^{0000}} = \bm{T_{20,0000}^{0000}} ,$$ (119)

$${}{G_{20,0011}^{0011}} = {}{T_{20,0011}^{0011}} ,$$ (120)

$${}{G_{22,0011}^{0011}} = {}{T_{22,0011}^{0011}} ,$$ (121)

and of four terms corresponding to the independent coupling constants:

$${}{G_{00,1101}^{1101}} = {}{T_{00,1101}^{1101}}-\bm{T_{00,2000}^{0000}} ,$$ (122)

$${}{G_{11,0011}^{1101}} = {}{T_{11,0011}^{1101}}+\bm{T_{11,1111}^{0000}} ,$$ (123)

$${}{G_{00,2011}^{0011}} = -\tfrac{1}{3}\bm{T_{00,1110}^{1110}}-\tfrac{1}{\sqrt{3}}\bm{T_{00,1111}^{1111}}$$

$$-\tfrac{1}{3} \sqrt{5} \bm{T_{00,1112}^{1112}}+{}{T_{00,2011}^{0011}} ,$$ (124)

$${}{G_{00,2211}^{0011}} = -\tfrac{1}{3} \sqrt{5} \bm{T_{00,1110}^{1110}}+\tfrac{1}{2} \sqrt{\tfrac{5}{3}} \bm{T_{00,1111}^{1111}}$$

$$-\tfrac{1}{6}\bm{T_{00,1112}^{1112}}+{}{T_{00,2211}^{0011}} .$$ (125)

Again, terms that depend on time-even densities are marked by using the bold-face font. Altogether, 7 free coupling constants (3 unrestricted and 4 independent) define the Galilean or gauge invariant EDF at second order, cf. Table 6.