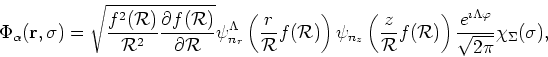Next: HFB Diagonalization in Configurational
Up: Axially Deformed Nuclei
Previous: Axially Deformed Nuclei
HO and THO Wave Functions
The solution of the HFB equation (16) is obtained by expanding
the quasiparticle function (24) in a given complete set of
basis wave functions that conserve axial symmetry and parity.
The
program HFBTHO (v1.66p) is able to do so for the two basis sets of
wave functions: HO and THO.
The HO set consists of eigenfunctions of a single-particle
Hamiltonian for an axially deformed harmonic oscillator potential.
By using the standard oscillator constants:
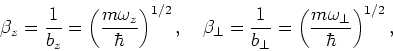 |
(27) |
and auxiliary variables
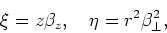 |
(28) |
the HO eigenfunctions are written explicitly as
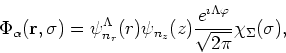 |
(29) |
where
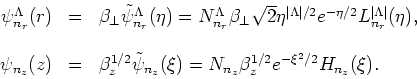 |
(30) |
 and
and
 denote the Hermite and
associated Laguerre polynomials [31], respectively,
and the normalization factors read
denote the Hermite and
associated Laguerre polynomials [31], respectively,
and the normalization factors read
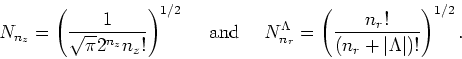 |
(31) |
The set of quantum numbers
 includes the numbers of nodes,
includes the numbers of nodes,  and
and  , in the
, in the  and
and  directions, respectively, and the projections on the
directions, respectively, and the projections on the  axis,
axis,
 and
and  , of the angular momentum operator and the spin.
, of the angular momentum operator and the spin.
The HO energy associated with the HO state (29) reads
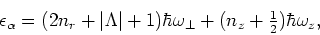 |
(32) |
and the basis used by the code consists of
 =
= +
+ +
+ +
+ states having the lowest
energies
states having the lowest
energies
 for the given frequencies
for the given frequencies
 and
and  . In this way, for the
spherical basis, i.e., for
. In this way, for the
spherical basis, i.e., for
 =
= , all HO shells
with the numbers of quanta
, all HO shells
with the numbers of quanta  =0...
=0... are included in the basis. When
the basis becomes deformed,
are included in the basis. When
the basis becomes deformed,

 ,
the code selects the lowest-HO-energy basis states by checking the HO
energies of all states up to 50 HO quanta. Note that in this case the
maximum value of the quantum number
,
the code selects the lowest-HO-energy basis states by checking the HO
energies of all states up to 50 HO quanta. Note that in this case the
maximum value of the quantum number  , and the number of
blocks in which the HFB equation is diagonalized, see
Sec. 3.4, depend on the deformation of the basis.
, and the number of
blocks in which the HFB equation is diagonalized, see
Sec. 3.4, depend on the deformation of the basis.
The THO set of basis wave functions consists of transformed harmonic
oscillator functions, which are generated by applying the local
scale transformation (LST) [19,32,20] to the HO
single-particle wave functions (29). In the axially deformed
case, the LST acts only on the cylindrical coordinates  and
and  , i.e.,
, i.e.,
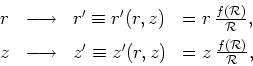 |
(33) |
and the resulting THO wave functions read
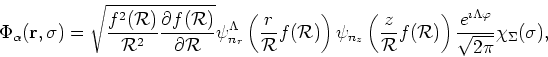 |
(34) |
where
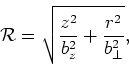 |
(35) |
and  is a scalar LST function. In the code HFBTHO
(v1.66p), function
is a scalar LST function. In the code HFBTHO
(v1.66p), function  is chosen as in
Ref. [23]. It transforms the incorrect Gaussian
asymptotic behavior of deformed HO wave functions into the correct
exponential form. Below, we keep the same notation
is chosen as in
Ref. [23]. It transforms the incorrect Gaussian
asymptotic behavior of deformed HO wave functions into the correct
exponential form. Below, we keep the same notation
 for both HO and THO wave functions, because expressions
in which they enter are almost identical in both cases and are valid
for both HO and THO variants.
for both HO and THO wave functions, because expressions
in which they enter are almost identical in both cases and are valid
for both HO and THO variants.



Next: HFB Diagonalization in Configurational
Up: Axially Deformed Nuclei
Previous: Axially Deformed Nuclei
Jacek Dobaczewski
2004-06-25
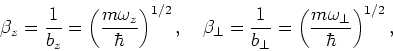
![]() and
and ![]() , i.e.,
, i.e.,