Skyrme Energy Density Functional

For Skyrme forces, the HFB energy (6) has the form of a local energy density functional,

$$E[\rho,\tilde{\rho}]=\int d^3{\bf r}~{\cal H}({\bf r}) ,$$ (9)

where

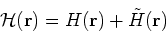$${\cal H}({\bf r})=H({\bf r})+\tilde{H}({\bf r})$$ (10)

is the sum of the mean-field and pairing energy densities. In the present implementation, we use the following explicit forms:

$$\begin{array}{rll} H({\bf r}) & = & {\textstyle{\frac{\hbar^... ...left. \rho_{q}{\bf\nabla }_{k}{\bf J}_{q,ij}\right] \end{array}$$ (11)

and

$$\displaystyle \tilde{H}({\bf r}) = {\textstyle{\frac{1}{2}}}... ...}\right)^\gamma~ \right]\sum\limits_{q}\tilde{\rho}_{q}^{2} .$$ (12)

Index $q$ labels the neutron ($q=n$) or proton ($q=p$) densities, while densities without index $q$ denote the sums of proton and neutron densities. $H({\bf r})$ and $\tilde{H}({\bf r})$ depend on the particle local density $\rho ({\bf r})$, pairing local density $\tilde{\rho}({\bf r})$, kinetic energy density $\tau ({\bf r})$, and spin-current density ${\bf J}_{ij}({\bf r})$:

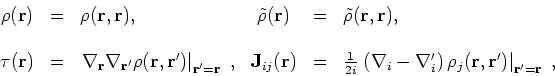$$\begin{array}{c} \begin{array}{ccl} \rho ({\bf r}) & = & \rh... ...ght\vert _{{\bf r}^{\prime }{\bf =r}}\;, \end{array}\end{array}$$ (13)

where $\rho ({\bf r},{\bf r}^{\prime }),\,\rho_{i}({\bf r},{\bf r}^{\prime }),\,\tilde{\rho}({\bf r},{\bf r}^{\prime }),\,\tilde{\rho}_{i}({\bf r},{\bf r}^{\prime })$ are defined by the spin-dependent one-body density matrices in the standard way:

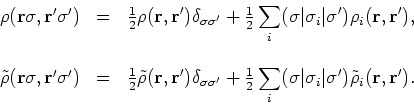$$\begin{array}{rcl} \rho ({\bf r}\sigma ,{\bf r^{\prime }}\si... ...me })\tilde{\rho}_{i}( {\bf r},{\bf r}^{\prime }) . \end{array}$$ (14)

We use the pairing density matrix $\tilde{\rho}$,

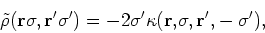$$\tilde{\rho}({\bf r}\sigma ,{\bf r^{\prime }}\sigma^{\prime ... ...\kappa ({\bf r,}\sigma ,{\bf r^{\prime },}-\sigma^{\prime }) ,$$ (15)

instead of the pairing tensor $\kappa$. This is convenient when describing time-even quasiparticle states when both $\rho$ and $\tilde{\rho}$ are hermitian and time-even [2]. In the pairing energy density (12), we have restricted our consideration to contact delta pairing forces in order to reduce the complexity of the general expressions [2,28].