Local densities

In the Skyrme-HFB formalism, the evaluation of the expectation value of the energy leads to an expression which is a functional of the local densities, namely, the particle (normal) and pairing (abnormal) densities

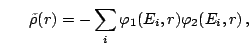$$\rho(r) = \sum_{i} \varphi_2(E_i,r)^2 \hskip 5mm \hskip 6mm \tilde\rho(r) = -\sum_{i} \varphi_1(E_i,r)\varphi_2(E_i,r)\,,$$ (4)

and their derivatives. The presence of non local terms in the force leads to a dependence on the normal and abnormal kinetic densities

$$\tau({\mathbf r}) = \displaystyle \sum_{i} \left\vert\boldsymbol\nabla\varphi_2(E_i,{\mathbf r})\right\vert^2\,, \hfill$$ (5)

$$\tilde\tau({\mathbf r}) = \displaystyle -\sum_{i} \boldsymbol\nabla\varphi_1(E_i,{\mathbf r})\cdot \boldsymbol\nabla\varphi_2(E_i,{\mathbf r})\,,$$ (6)

while the spin-orbit term leads to a dependence on the spin current tensors ${\mathbb{J}}_{ij}$ and $\tilde{\mathbb{J}}_{ij}$. We do not give here the definitions of these tensors, because for the spherical symmetry discussed here they reduce to the corresponding spin current vectors ${\mathbf J}$ and $\tilde{\mathbf J}$

$$\mathbf J({\mathbf r}) = \displaystyle \mathrm{i}\sum_{i} \varphi_2(E_i,{\mathbf r}) {\bol... ...athbf r}) \langle \sigma'\vert\hat{\boldsymbol\sigma}\vert\sigma\rangle, \hfill$$ (7)

$$\tilde{\mathbf J}({\mathbf r}) = \displaystyle -\mathrm{i}\sum_{i} \varphi_1(E_i,{\mathbf r}) {\bo... ...E_i,{\mathbf r}) \langle \sigma'\vert\hat{\boldsymbol\sigma}\vert\sigma\rangle.$$ (8)