Figures

  

Figure 1: One-neutron separation energies S_N (a) and the spherical s.p. energies (b) in heavy carbon isotopes. Spherical self-consistent HFB and HF calculations have been performed for the Skyrme SLy4 interaction [25]. Experimental (EXP) and systematics (SYS) separation energies are taken from Ref.[24].

  

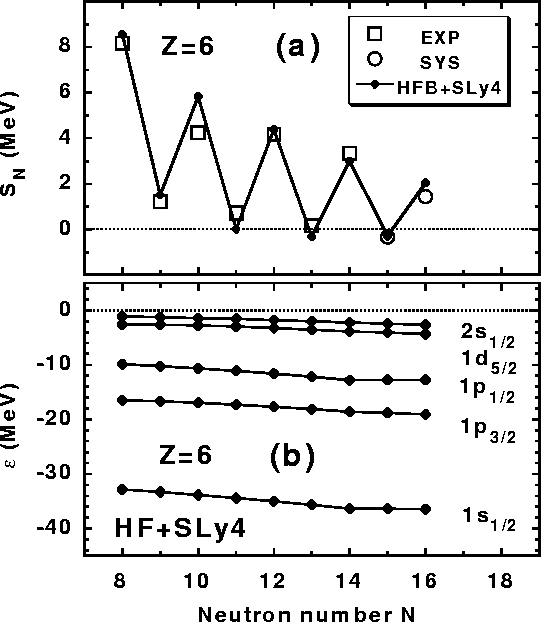Figure 2: Results of the spherical HFB calculations performed for the model PTG s.p. spectrum with varying positions of the 2s_1/2 level. Panel (a) shows the HFB canonical s.p. energies (open squares), the PTG s.p. energies of the bound 2s_1/2 states (full circles) and the real parts of the 2s_1/2 resonances (open circles). The HFB neutron rms radius (b), average pairing gap $\langle\Delta\rangle$ (c), and average neutron number $\langle{N}\rangle$ (d) (full squares in panels (b)-(d)), were calculated for a fixed value of the neutron Fermi energy of $\lambda$=-0.056MeV. The corresponding canonical pairing gap (c) and average neutron number (d) are shown with open squares. The no-pairing PTG rms radius in panel (b) corresponds to N=16.

  

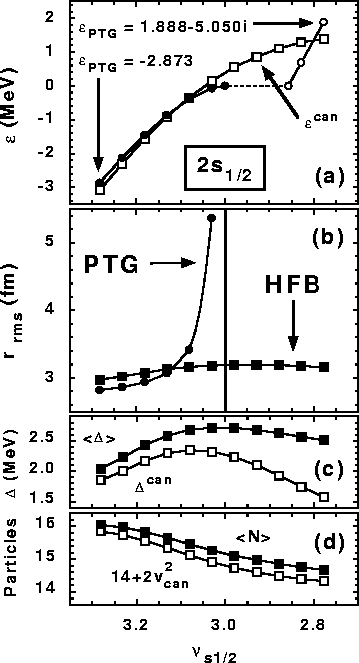Figure 3: Contributions N(E) and r²(E) to the average neutron number and radius squared, respectively, calculated for the HFB q.p. states, as functions of the q.p. energy E. The HFB calculations have been performed at a fixed Fermi energy of $\lambda$=-0.056MeV. The curves correspond to calculations performed for different positions of the 2s_1/2 PTG states, with the s.p. energies indicated explicitly [see also Fig. 2(a)].