


Next: Shape-current orientation
Up: Isospin-breaking corrections to superallowed
Previous: Numerical details
ISB corrections to the superallowed
 Fermi transitions
Fermi transitions
The
 Fermi
Fermi  -decay proceeds between
the ground state (g.s.) of the even-even nucleus
-decay proceeds between
the ground state (g.s.) of the even-even nucleus
 and its isospin-analogue partner
in the
and its isospin-analogue partner
in the  odd-odd nucleus,
odd-odd nucleus,
 . The corresponding transition matrix element is:
. The corresponding transition matrix element is:
 |
(17) |
The g.s. state
 in Eq. (17) is approximated by a projected state
in Eq. (17) is approximated by a projected state
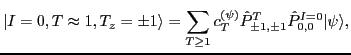 |
(18) |
where
 is the g.s. of the even-even nucleus obtained in self-consistent MF calculations.
The state
is the g.s. of the even-even nucleus obtained in self-consistent MF calculations.
The state
 is unambiguously defined by filling in the pairwise
doubly degenerate levels of protons and neutrons up to the Fermi level.
The daughter state
is unambiguously defined by filling in the pairwise
doubly degenerate levels of protons and neutrons up to the Fermi level.
The daughter state
 is approximated by
is approximated by
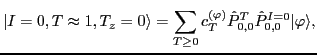 |
(19) |
where the self-consistent Slater determinant
 (or
(or
 )
represents the so-called anti-aligned configuration,
selected by placing the odd neutron and the odd proton in
the lowest available time-reversed (or signature-reversed) s.p. orbits.
The s.p. configuration
)
represents the so-called anti-aligned configuration,
selected by placing the odd neutron and the odd proton in
the lowest available time-reversed (or signature-reversed) s.p. orbits.
The s.p. configuration
 manifestly breaks the
isospin symmetry as schematically depicted
in Fig. 1. The isospin projection from
manifestly breaks the
isospin symmetry as schematically depicted
in Fig. 1. The isospin projection from
 as expressed by Eq. (19) is essentially the only way
to reach the
as expressed by Eq. (19) is essentially the only way
to reach the
 states in odd-odd
states in odd-odd  nuclei.
nuclei.
Figure 1:
Left: two possible g.s. configurations of an odd-odd  =
= nucleus, as described by the
conventional deformed MF theory. These degenerate configurations are
called aligned (upper) and anti-aligned (lower), depending on what
levels are occupied by the valence particles. The right panel shows
what happens when the isospin-symmetry is restored. The aligned
configuration is isoscalar; hence, it is insensitive to the isospin
projection. The anti-aligned configuration represents a mixture of
nucleus, as described by the
conventional deformed MF theory. These degenerate configurations are
called aligned (upper) and anti-aligned (lower), depending on what
levels are occupied by the valence particles. The right panel shows
what happens when the isospin-symmetry is restored. The aligned
configuration is isoscalar; hence, it is insensitive to the isospin
projection. The anti-aligned configuration represents a mixture of
 =0 and
=0 and  =1 states. The isospin projection removes the
degeneracy by lowering the
=1 states. The isospin projection removes the
degeneracy by lowering the  =0 level.
=0 level.
![\includegraphics[width=0.8\columnwidth]{deltaC.fig01.eps}](img129.png) |
Subsections



Next: Shape-current orientation
Up: Isospin-breaking corrections to superallowed
Previous: Numerical details
Jacek Dobaczewski
2012-10-19
![]() Fermi
Fermi ![]() -decay proceeds between
the ground state (g.s.) of the even-even nucleus
-decay proceeds between
the ground state (g.s.) of the even-even nucleus
![]() and its isospin-analogue partner
in the
and its isospin-analogue partner
in the ![]() odd-odd nucleus,
odd-odd nucleus,
![]() . The corresponding transition matrix element is:
. The corresponding transition matrix element is:
![]() in Eq. (17) is approximated by a projected state
in Eq. (17) is approximated by a projected state
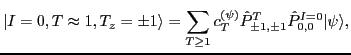
![\includegraphics[width=0.8\columnwidth]{deltaC.fig01.eps}](img129.png)