Center-of-mass correction to the energy

Since the HF or HFB states break the translational symmetry, one has to add, in principle, to the total energy the so-called center-of-mass correction [18],

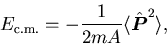$$E_{\mbox{\scriptsize {c.m.}}} = -\frac{1}{2mA}\langle\hat{\mbox{{\boldmath {$P$}}}}^2\rangle ,$$ (15)

where $\hat{\mbox{{\boldmath {$P$}}}}$= $-i\hbar\sum_{i=1}^A\nabla_i$ is the total linear momentum operator. Since evaluation of this correction is time consuming, one often uses the approximation which keeps only the direct term, i.e.,

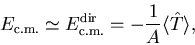$$E_{\mbox{\scriptsize {c.m.}}} \simeq E^{\mbox{\scriptsize {d... ...ox{\scriptsize {c.m.}}} = -\frac{1}{A}\langle\hat{T}\rangle ,$$ (16)

where $\hat{T}$= $-\frac{\hbar^2}{2m}\sum_{i=1}^A\nabla^2_i$ is the one-body kinetic-energy operator. Within this approximation, a simple renormalization of the nucleon mass,

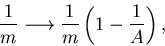$$\frac{1}{m} \longrightarrow \frac{1}{m}\left(1-\frac{1}{A}\right),$$ (17)

allows to include correction (19) before variation. This way of proceeding is traditionally most often employed, and it has also been implemented by default in previous versions of the code HFODD. A more advanced, while still not-too-expensive method consists in evaluating correction (18) after variation, i.e., after having performed the HF or HFB iterations. Such an option has now been implemented in version (v2.07f).