Spin-orbit and tensor forces

Momentum-dependent two-body SO[8] and tensor[9,10] interactions have the form

$$\begin{array}{rcl} \hat{V}_{SO} &=& iW_0 \hat{\mbox{\boldmat... ...f S}} \cdot\hat{\mbox{\boldmath${k}$\unboldmath }}, \end{array}$$ (1)

where the vector and tensor spin operators read

$$\begin{array}{rcl} \hat{\mbox{\boldmath${S}$\unboldmath }} &... ... }_1\cdot\mbox{\boldmath${\sigma}$\unboldmath }_2 . \end{array}$$ (2)

When averaged with one-body density matrices, these interactions contribute to the following terms in the EDF (see Refs.[16,4] for derivations),

$$\begin{array}{rcl} {\mathcal H}_{SO} &=& {\textstyle{\frac{1... ...}\Big[t_e{J}_n{J}_p +t_o({J}_0^2-{J}_n{J}_p)\Big] , \end{array}$$ (3)

where the conservation of time-reversal and spherical symmetries was assumed. Here, $\rho_t$ and ${J}_t$ are the neutron, proton, isoscalar, and isovector particle and SO densities[8,16,4] for $t$=$n$, $p$, 0, and 1, respectively.

Apart from the contribution of the SO energy density to the central potential, variation of the SO and tensor terms with respect to the densities yields the one-body SO potential for neutrons ($t$=$n$) and protons ($t$=$p$),

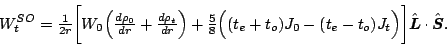$$W^{SO}_t = {\textstyle{\frac{1}{2r}}}\bigg[ W_0\Big({\textst... ...}$\unboldmath }}\cdot\hat{\mbox{\boldmath${S}$\unboldmath }} .$$ (4)

Hence, it is clear that the only effect of including the tensor interaction is a modification of the SO splitting of the single-particle levels, and that, from the point of view of one-body properties, tensor interactions act very similarly to the two-body SO interactions. However, the latter ones induce the SO splitting that is only weakly depending on the shell filling. This is so because the corresponding form-factor in Eq. (4) is given by the radial derivatives of densities. On the other hand, the SO splitting induced by the tensor forces depends strongly on the shell filling, because its form-factor is given by the SO densities $J(r)$. Indeed, when only one of the SO partners is occupied (SUS system), the SO density is large, and when both partners are occupied (SS system), the SO density is small, see Sec. 4 for numerical examples.