Determination of effective s.p. observables

Once the averages of physical observables $O(k)$ for the set of $N_c$ calculated configurations ($k=1,\dots,N_c$) are determined, the effective s.p. contributions $o^{\mbox{\rm\scriptsize {eff}}}_{\alpha}$ (19) are found by means of a multivariate least-square fit (see, e.g., Refs. [29,30]). This is done by minimizing the function of $o^{\mbox{\rm\scriptsize {eff}}}_{\alpha}$ defined by

$$F\left[o^{\mbox{\rm\scriptsize {eff}}}_{\alpha}\right]=\sum_... ...lpha}^{\mbox{\rm\scriptsize {eff}}} c_{\alpha}(k) \right )^2 .$$ (22)

Note that the problem is only meaningful when the number of configurations is sufficiently large, $N_c > m$. Following the general concept of the least-square method, the partial differentiation with respect to the variables $o^{\mbox{\rm\scriptsize {eff}}}_{\alpha}$ yields

$$0 = \frac{1}{2} \frac{\partial}{\partial o_{\alpha}^{\mbox{\rm\scriptsize {eff}}}} F\left[o^{\mbox{\rm\scriptsize {eff}}}_{\alpha}\right] = {}$$

$$= \sum_{\alpha'} \sum_{k} c_{\alpha}(k) c_{\alpha'}(k) o^{\mbox{\rm\scriptsize {eff}}}_{\alpha'} -\sum_{k} \delta O(k) c_{\alpha}(k)=$$

$${} = (Bo^{\mbox{\rm\scriptsize {eff}}}-a)_{\alpha} ,$$ (23)

where $a_{\alpha}=\sum_k \delta O(k) c_{\alpha}(k) = c^T \delta O$ and $B=\vert\vert B_{\alpha \alpha'}\vert\vert= \vert\vert\sum_k c_{\alpha}(k) c_{\alpha'}(k) \vert\vert=c^Tc$. Solving this equation by inverting the non-singular matrix $B$ gives the solution to the multivariate regression problem:

$$\tilde{o}^{\mbox{\rm\scriptsize {eff}}} = B^{-1}a=(c^T c)^{-1} c^T \delta O.$$ (24)

The fact that $B$ is positive-definite guarantees that the solution $\tilde{o}^{\mbox{\rm\scriptsize {eff}}}$ corresponds to a minimum of $F\left[o^{\mbox{\rm\scriptsize {eff}}}_{\alpha}\right]$.

In order to estimate the variance, we assume that the first statistical moments of residuals,

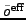$$\epsilon_O(k) = \delta O(k) - \sum_{\alpha} c_{\alpha}(k) \tilde{o}_{\alpha}^{\mbox{\rm\scriptsize {eff}}},$$ (25)

are zero for all $k=1,...,N_c$. Consequently, $\tilde{o}^{\mbox{\rm\scriptsize {eff}}}$ can be considered an unbiased estimate of $o^{\mbox{\rm\scriptsize {eff}}}$. Furthermore, under the assumption that

$$\mbox{\rm\scriptsize {var}}(\epsilon_O(k))=\sigma^2$$ (26)

for all $k=1,\ldots,N_c$, and

$$\mbox{\rm\scriptsize {cov}}(\epsilon_O(k),\epsilon_O(k'))=0$$ (27)

for all $\{k,k'=1,\ldots,N_c\vert k \neq k'\}$, one can define the variance-covariance matrix as $\sigma^2 B^{-1}= \sigma^2 (c^Tc)^{-1}$, for which the unbiased estimate for $\sigma^2$ is given by

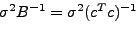$$\tilde{\sigma}^2 = \frac {1}{N_c-m} \sum_{k=1}^{N_c} \epsilon_O(k)^2.$$ (28)

Finally, the unbiased estimate for the variance-covariance matrix for $\tilde{o}^{\mbox{\rm\scriptsize {eff}}}$ is given by $B^{-1}\sigma^2$. In what follows we do not differentiate between notations for variables and their estimates. The least-square procedure described in this section was used to determine the effective s.p. quadrupole moments $\{q_{20,\alpha}^{\mbox{\rm\scriptsize {eff}}},q_{22,\alpha}^{\mbox{\rm\scriptsize {eff}}}, q_{t,\alpha}^{\mbox{\rm\scriptsize {eff}}}, \alpha=1,...,m\}$ and angular momentum alignments $\{j_{\alpha}^{\mbox{\rm\scriptsize {eff}}}, \alpha=1,...,m\}$.