Additivity of effective s.p. observables

For each $k$-configuration defined by occupying a given set of s.p. orbitals and represented by a product state $\vert k\rangle$, we determine the average value $O(k)=\langle{k}\vert\hat{O}\vert k\rangle$ of a s.p. operator $\hat{O}$. We may now designate one of these configurations as a reference, or a core configuration, and determine the relative change $\delta O(k) \equiv O(k) - Q^{\mbox{\rm\scriptsize {core}}}$ of the physical observable in the $k$-th configuration with respect to that in the core configuration. The additivity principle stipulates that all these differences can be expressed as sums of individual effective contributions $o^{\mbox{\rm\scriptsize {eff}}}_{\alpha}$ coming from s.p. states (enumerated by index $\alpha$), i.e.,

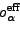$$O(k) - Q^{\mbox{\rm\scriptsize {core}}} \equiv \delta O(k) =... ...{\alpha}c_{\alpha}(k)o^{\mbox{\rm\scriptsize {eff}}}_{\alpha}.$$ (19)

Coefficients $c_{\alpha}$ in Eq. (19) define the s.p. content of the configuration $k$ with respect to the core configuration. Namely,

(i)

$c_{\alpha}(k)=0$ if the state $\alpha$ is not occupied in either of these two configurations, or is occupied in both of them,

(ii)

$c_{\alpha}(k)=1$ if $\alpha$ has a particle character (it is occupied in the $k$-th configuration and is not occupied in the core configuration),

(iii)

$c_{\alpha}(k)=-1$ if the state $\alpha$ has a hole character (it is not occupied in the $k$-th configuration and is occupied in the core configuration).

In this way, one can label the $k$-th configuration with the set of coefficients $c(k) = \{c_{\alpha}(k), \alpha = 1, \dots ,m\}$, where $m$ denotes the size of s.p. space considered. The values of $o^{\mbox{\rm\scriptsize {eff}}}_{\alpha}$ can be calculated by proceeding step by step from the core configuration to the configurations differing by one particle or one hole, then to the configurations differing by two particles, two holes, or a particle and a hole, and so forth, until the data set is generated which is statistically large enough to provide appreciable precision for $o_\alpha^{\mbox{\rm\scriptsize {eff}}}$. Had the additivity principle been obeyed exactly, calculations limited to one-particle and one-hole configurations would have sufficed. Since our goal is not only to determine values of $o^{\mbox{\rm\scriptsize {eff}}}_{\alpha}$ but actually prove that the additivity principle holds up to a given accuracy, we have to consider a large set of configurations and determine the best values of $o^{\mbox{\rm\scriptsize {eff}}}_{\alpha}$ together with their error bars.

In what follows, we consider relative changes in the average quadrupole moments $\delta Q_{20}(k)$ and $\delta Q_{22}(k)$, transition quadrupole moments $\delta Q_t(k)$, and total angular momenta $\delta J(k)$ (see Sec. 2.1), which are related to the effective one-body expectation values via the additivity principle.

The addition of particle or hole in a specific single-particle orbital $\alpha$ gives rise to a polarization of the system, so the effective s.p. values, $o^{\mbox{\rm\scriptsize {eff}}}_{\alpha}$, depend not only on the bare s.p. expectation values, $o^{\mbox{\rm\scriptsize {bare}}}_{\alpha}=\left< \hat{o}\right>_{\alpha}$, but also contain polarization contributions. For example, the effective s.p. charge quadrupole moment $q_{20,\alpha}^{\mbox{\rm\scriptsize {eff}}}$ can be represented as the sums of bare s.p. charge quadrupole moments $q_{20,\alpha}^{\mbox{\rm\scriptsize {bare}}}=\left< \hat{q}_{20} \right>_{\alpha}$ and polarization contributions $q^{\mbox{\rm\scriptsize {pol}}}_{20,\alpha}$:

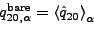$$q^{\mbox{\rm\scriptsize {eff}}}_{20,\alpha} = q^{\mbox{\rm\... ...}}_{20,\alpha} + q^{\mbox{\rm\scriptsize {pol}}}_{20,\alpha} .$$ (20)

Therefore, for neutron orbitals, which have vanishing bare charge quadrupole moments, $q^{\mbox{\rm\scriptsize {bare}}}_{20,\alpha_n}=0$, the effective charge quadrupole moments are solely given by polarization terms:

$$q^{\mbox{\rm\scriptsize {eff}}}_{20,\alpha_n} = q^{\mbox{\rm\scriptsize {\mbox{\rm\scriptsize {pol}}}}}_{20,\alpha_n} .$$ (21)