Spin and isospin polarized infinite nuclear matter

Let us consider the infinite nuclear matter with spin and isospin polarizations, which is described by the one-body Hamiltonian,

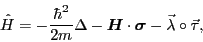$$\hat{H}= -\frac{\hbar^2}{2m}\Delta - \bbox{H}\cdot\bbox{\sigma} - \vec{\lambda}\circ\vec{\tau},$$ (69)

where $\bbox{\sigma}$ and $\bbox{H}$ are the space vectors of spin Pauli matrices and spin-polarization Lagrange multipliers, respectively, and $\vec{\tau}$ and $\vec{\lambda}$ are the isovectors of the analogous isospin Pauli matrices and isospin-polarization Lagrange multipliers, whereas the dot ``$\cdot$'' (circle ``$\circ$'') denotes the scalar (isoscalar) product. Each eigenstate of Hamiltonian (69) is a Slater determinant that depends on the orientations of the Lagrange multipliers $\bbox{H}$ and $\vec{\lambda}$ in the space and isospace, respectively. However, since the kinetic energy is scalar and isoscalar, we can arbitrarily fix these orientations to $\bbox{H}_z$ and $\vec{\lambda}_3$, which gives the nonlocal densities for spin-up and spin-down ($\sigma=\pm1$) neutrons and protons ($\tau=\pm1$) in the form,

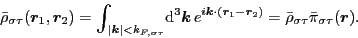$$\bar{\rho}_{\sigma\tau}(\bboxr_1,\bboxr_2) = {\bigint\raiseb... ...{\sigma\tau}\bar{\pi}_{\sigma\tau}(\mbox{{\boldmath {$r$}}}) .$$ (70)

The system simply separates into four independent Fermi spheres for spin-up and spin-down neutrons and protons, with four constant densities $\bar{\rho}_{\sigma\tau}$, whereas the dependence on the relative position vector $\mbox{{\boldmath {$r$}}}$ is given by four scalar functions $\bar{\pi}_{\sigma\tau}(r)$ [compare Eq. (30)],

$$\bar{\pi}_{\sigma\tau}(r) = \frac{3j_1(k_{F,\sigma\tau}r)}{k_{F,\sigma\tau}r} .$$ (71)

We note that the spin-isospin indices $\sigma\tau$ pertain here to the preselected quantization axis defined by the chosen directions of $\bbox{H}$ and $\vec{\lambda}$, which define an ``intrinsic'' reference frame. In this reference frame, densities are marked with a bar symbol.

The ground state of the system is obtained by filling the four Fermi spheres up to the common Fermi energy $\epsilon_F$,

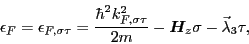$$\epsilon_F = \epsilon_{F,\sigma\tau} = \frac{\hbar^2k_{F,\sigma\tau}^2}{2m} - \bbox{H}_z\sigma - \vec{\lambda}_3\tau,$$ (72)

which defines the four Fermi momenta $k_{F,\sigma\tau}$. Finally, by varying $\epsilon_F$, one obtains systems with different total densities $\rho=\sum_{\sigma\tau}\bar{\rho}_{\sigma\tau}$.

It is, of course, clear that for the asymmetric and polarized infinite nuclear matter, the density matrix of Eq. (39) is diagonal in spin and isospin,

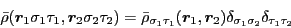$$\bar{\rho}(\bboxr_1\sigma_1\tau_1,\bboxr_2\sigma_2\tau_2) = ... ...xr_1,\bboxr_2) \delta_{\sigma_1\sigma_2} \delta_{\tau_1\tau_2}$$ (73)

and thus the nonlocal densities $\bar{\rho}_{\mu k}(\bboxr_1,\bboxr_2)$ have non-zero components only for $\mu=0$ or $z$ and $k=0$ or 3, that is,

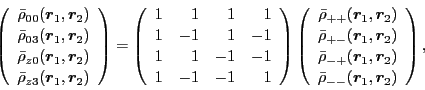$$\left(\begin{array}{c} \bar{\rho}_{00}(\bboxr_1,\bboxr_2) \\... ...) \\ \bar{\rho}_{--}&(\bboxr_1,\bboxr_2) \end{array}\right) ,$$ (74)

where we have abbreviated the indices of $\sigma\tau$ just to their signs. After expressing the right-hand side of this equation in terms nonlocal densities (70), one obtains:

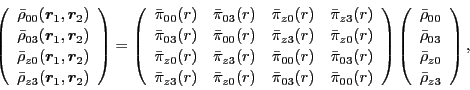$$\left(\begin{array}{c} \bar{\rho}_{00}(\bboxr_1,\bboxr_2) \\... ...} \\ \bar{\rho}_{z0} \\ \bar{\rho}_{z3} \end{array}\right) ,$$ (75)

where functions $\bar{\pi}_{\mu k}(r)$ are defined similarly as in Eq. (74), namely,

$$\left(\begin{array}{c} \bar{\pi}_{00}(r) \\ \bar{\pi}_{03}(... ...\bar{\pi}_{-+}&(r) \\ \bar{\pi}_{--}&(r) \end{array}\right) .$$ (76)

Already here we see the main problem: for the spin and isospin polarized systems, the spin-isospin channels of nonlocal densities $\bar{\rho}_{\mu k}(\bboxr_1,\bboxr_2)$ in Eq. (75) are linear combinations of the spin-isospin channels of local densities $\bar{\rho}_{\mu k}$; that is, the spin-isospin channels become mixed.

To make the preceding result even more clear, we note that the spin-isospin directions of the Lagrange multipliers $\bbox{H}$ and $\vec{\lambda}$ can be arbitrarily varied and the spin-isospin directions of the nonlocal densities $\rho_{\mu k}(\bboxr_1,\bboxr_2)$, local densities $\rho_{\mu k}$, and functions $\pi_{\mu k}(r)$ are always aligned with those of the Lagrange multipliers. Therefore, we can use the directions of the local densities instead of those pertaining to the Lagrange multipliers. By using the standard densities [19] in the (i) scalar-isoscalar channel ( $\rho=\rho_{00}$), (ii) vector-isoscalar channel ( $\bbox{s}_\mu=\rho_{\mu 0}$, for $\mu=x,y,z$), (iii) scalar-isovector channel ( $\vec{\rho}_k=\rho_{0 k}$, for $k=1,2,3$), and (iv) vector-isovector channel ( $\vec{\bbox{s}}_{\mu k}=\rho_{\mu k}$, for $\mu=x,y,z$ and $k=1,2,3$), we then define functions $\pi(r)$ in the four channels as,

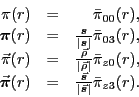$$\begin{array}{rll@{}l} \pi (r) &=& &\bar{\pi}_{00}(r), \\ \... ...x{s}}}{\vert\vec{\bbox{s}}\vert}&\bar{\pi}_{z3}(r). \end{array}$$ (77)

Here, the ``intrinsic'' functions $\bar{\pi}_{\mu k}(r)$ do not depend on the spin-isospin directions; that is, they are defined by the following Fermi energies,

$$\epsilon_F = \epsilon_{F,\sigma\tau} = \frac{\hbar^2k_{F,\si... ...m} - \vert\bbox{H}\vert\sigma - \vert\vec{\lambda}\vert\tau.$$ (78)

Finally, definitions (77) allow us to present densities in the ``laboratory'' reference frame as [compare Eq. (75)],

$$\rho(\bboxr_1,\bboxr_2) = \rho \,\pi(r) + \vec{\rho} \circ \vec{\pi}(r) + \bbox{s} \cdot \bbox{\pi}(r) + \vec{\bbox{s}}\cdot\circ\,\vec{\bbox{\pi}}(r) ,$$ (79)

$$\vec{\rho} (\bboxr_1,\bboxr_2) = \vec{\rho} \,\pi(r) + \rho \,\vec{\pi}(r) + \vec{\bbox{s}}\cdot\,\bbox{\pi}(r) + \bbox{s} \cdot \vec{\bbox{\pi}}(r) ,$$ (80)

$$\bbox{s} (\bboxr_1,\bboxr_2) = \bbox{s} \,\pi(r) + \vec{\bbox{s}}\circ\,\vec{\pi}(r) + \rho \,\bbox{\pi}(r) + \vec{\rho} \circ \vec{\bbox{\pi}}(r) ,$$ (81)

$$\vec{\bbox{s}}(\bboxr_1,\bboxr_2) = \vec{\bbox{s}}\,\pi(r) + \bbox{s} \,\vec{\pi}(r) + \vec{\rho} \,\bbox{\pi}(r) + \rho \,\vec{\bbox{\pi}}(r) .$$ (82)

Note that the same scalar-isoscalar function $\pi(r)$ multiplies all local densities in the first terms of Eqs. (79)-(82). Therefore, the postulate of using different functions in different channels [11] is not compatible with the results obtained for the polarized nuclear matter.

Again we see that the spin-isospin channels of nonlocal densities are mixed, namely, local densities in all channels contribute to every channel in the nonlocal density. As a consequence, the energy density is not invariant but only covariant with respect to the spin-isospin rotations (see the discussion in the Appendix A of Ref. [5]). Therefore, the NV expansion performed in the polarized nuclear matter does not lead to the standard local functional of Eq. (48). On the other hand, derivation in the unpolarized nuclear matter corresponds to all functions $\bar{\rho}_{\sigma\tau}(r)$ equal to one another, which leads to vanishing functions $\vec{\pi}(r)$, $\bbox{\pi}(r)$, and $\vec{\bbox{\pi}}(r)$. Then, in Eqs. (79)-(82), only the first terms survive and the spin-isospin channels are not mixed. Such a situation corresponds to postulating a channel-independent function $\pi(r)$, which we employed in Sec. 3.