Wstecz: 12.3 Zwalnianie pamięci — operator W górę: 12. Zarządzanie pamięcią Dalej: 12.5 Zarządzanie pamięcią w C
Pokazaliśmy, jak można dynamicznie alokować pamięć na tablice jednowymiarowe lub wielowymiarowe, ale takie w których tylko jeden, mianowicie pierwszy, wymiar nie jest z góry znany. Często jednak zachodzi potrzeba dynamicznego tworzenia tablic wielowymiarowych, na przykład dwuwymiarowych, ale takich, w których wszystkie wymiary są określane dynamicznie w trakcie wykonania programu. Pokażemy teraz jeden ze sposobów, w jaki można to zadanie zrealizować.
Załóżmy, że chcemy zaalokować miejsce na tablicę liczb typu double o wymiarach 2×3. Chcielibyśmy odnosić się do tej tablicy za pomocą normalnej składni z użyciem indeksów w nawiasach kwadratowych. Na przykład m[1][2] powinno oznaczać element z wiersza drugiego i kolumny trzeciej — indeksy liczymy jak zwykle od zera — tablicy (macierzy) m.
Co oznacza m[1][2]? Wiemy, że jest to skrócony zapis wyrażenia ' *(m[1] + 2)' (patrz rozdział o arytmetyce wskaźników ). Zatem m[1] musi być wskaźnikiem typu double*. A zatem m jest tablicą wskaźników, której kolejne elementy wskazują na początki kolejnych wierszy. A co to jest m[1]? To z kolei ' *(m + 1)'; skoro wartością tego wyrażenia ma być wskaźnik typu double*, to samo m musi być wskaźnikiem do wskaźnika, a więc mieć typ double**.
Możemy to przedstawić na rysunku:
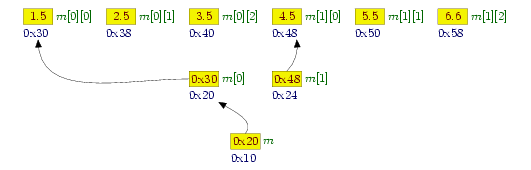
W rzędzie środkowym mamy dwuelementową tablicę wskaźników. Wartościami są adresy początków wierszy właściwej tablicy liczb. Elementy tej tablicy, jako wskaźniki, są czterobajtowe (lub ośmiobajtowe na platformie 64-bitowej): adresy kolejnych elementów odległe są zatem o cztery bajty.
W dolnym rzędzie mamy pojedynczą zmienną m, której wartością jest z kolei adres tablicy ze środkowego rzędu, a więc adres tablicy wskaźników typu double*. Zatem jest to wskaźnik do wskaźnika: typ m to double**.
Zobaczmy, jak można to zrealizować w programie:
1. #include <iostream>
2. using namespace std;
3.
4. double** allocMatrix2D(size_t,size_t);
5. void deleteMatrix2D(double**&);
6.
7. int main() {
8.
9. size_t dim1 = 2, dim2 = 3; // NIE stałe!
10.
11. // alokowanie
12. double** matrix2d = allocMatrix2D(dim1,dim2); ➊
13.
14. // wpisywanie wartości
15. for (size_t i = 0; i < dim1; ++i) ➋
16. for (size_t j = 0; j < dim2; ++j)
17. matrix2d[i][j] = 3*i+j+1.5;
18.
19. // drukowanie
20. for (size_t i = 0; i < dim1; ++i) {
21. for (size_t j = 0; j < dim2; ++j)
22. cout << matrix2d[i][j] << " ";
23. cout << endl;
24. }
25.
26. // usuwanie
27. deleteMatrix2D(matrix2d); ➌
28. }
29.
30. double** allocMatrix2D(size_t dim1, size_t dim2) { ➍
31. double** matrix2d = new double*[dim1];
32. double* dumm = new double[dim1*dim2];
33.
34. for (size_t i = 0; i < dim1; ++i)
35. matrix2d[i] = dumm + i*dim2;
36.
37. return matrix2d;
38. }
39.
40. void deleteMatrix2D(double**& matrix2d) { ➎
41. delete [] matrix2d[0];
42. delete [] matrix2d;
43. matrix2d = 0;
44. }
Dwywymiarowa tablica (macierz) jest tworzona przez funkcję allocMatrix2D (➍). Zmienne dim1 i dim2 oznaczają wymiary tablicy: dim1 jest liczbą wierszy, dim2 liczbą kolumn.
Najpierw tworzymy zmienną matrix2d typu double** i wpisujemy tam adres zaalokowanej tablicy wskaźników typu double*. Liczba tych wskaźników odpowiada liczbie wierszy w macierzy. Na rysunku zmienna m odpowiada zmiennej macierz2d, a tablica ze środkowego rzędu odpowiada tablicy wskaźników wskazywanej przez matrix2d.
Następnie tworzymy właściwą tablicę liczb. Ich ilość to iloczyn wymiarów. Adres zawarty w dumm to adres początku tej tablicy (na rysunku jest to adres 0x30).
Teraz w pętli wypełniamy tablicę wskaźników ze środkowego rzędu na rysunku: do kolejnych elementów wpisujemy adresy początków wierszy tablicy liczb. Są one od siebie odległe o tyle wielokrotności długości jednej zmiennej typu double, ile wynosi liczba kolumn (u nas jest to dim2), czyli jak długi jest jeden wiersz.
Do funkcji wywołującej zwracamy wartość zmiennej matrix2d, która może być używana zgodnie ze składnią macierzową.
W programie głównym używamy tej macierzy: wpisujemy wartości i drukujemy testowe wyniki
1.5 2.5 3.5
4.5 5.5 6.5
Po użyciu naszej macierzy, w linii ➌ usuwamy ją wywołując funkcję
deleteMatrix2d
(➎). W funkcji tej musimy wywołać operator
delete
dwa razy, bo tyle razy użyliśmy operatora
new
konstruując macierz. Najpierw zwalniamy tablicę liczb — jej adres to
adres początku pierwszego wiersza (o numerze 0), a zatem jest to adres
zawarty w
macierz2d[0]. Potem zwalniamy tablicę wskaźników
wskazywaną przez
macierz2d. Kolejność jest tu istotna: gdybyśmy
usunęli najpierw tablicę wskaźników, to do tablicy liczb nie mielibyśmy
już dostępu. Na zakończenie zerujemy na wszelki wypadek wskaźnik
macierz2d. Przesłaliśmy go do funkcji przez referencję,
aby to wyzerowanie było skuteczne również w funkcji wywołującej.
W podobny sposób można budować tablice więcej niż dwuwymiarowe.
Na przykład poniższy program pokazuje, jak można to zrobić dla
macierzy dwu-, trzy- i czterowymiarowych (tym razem są to macierze
liczb całkowitych):
1. #include <iostream>
2. using namespace std;
3.
4. int** allocMatrix2D(int,int);
5. void deleteMatrix2D(int**&);
6.
7. int*** allocMatrix3D(int,int,int);
8. void deleteMatrix3D(int***&);
9.
10. int**** allocMatrix4D(int,int,int,int);
11. void deleteMatrix4D(int****&);
12.
13. int main() {
14. int dim1 = 7, dim2 = 9, dim3 = 12, dim4 = 5;
15.
16. // Macierze dwuwymiarowe //////////////////
17.
18. // alokowanie
19. int** matrix2d = allocMatrix2D(dim1,dim2);
20.
21. // test
22. for ( int i = 0; i < dim1; i++ )
23. for ( int j = 0; j < dim2; j++ )
24. matrix2d[i][j] = i+j+2;
25.
26. cout << "Macierz dwuwymiarowa" << endl
27. << " Element srodkowy: "
28. << matrix2d[dim1/2][dim2/2] << endl
29. << " Powinno byc : "
30. << dim1/2 + dim2/2 +2 << endl;
31. cout << " Element ostatni : "
32. << matrix2d[dim1-1][dim2-1] << endl
33. << " Powinno byc : "
34. << dim1 + dim2 << endl << endl;
35.
36. // usuwanie
37. deleteMatrix2D(matrix2d);
38.
39. // Macierze trzywymiarowe ///////////////////////
40.
41. // alokowanie
42. int*** matrix3d = allocMatrix3D(dim1,dim2,dim3);
43.
44. // test
45. for ( int i = 0; i < dim1; i++ )
46. for ( int j = 0; j < dim2; j++ )
47. for ( int k = 0; k < dim3; k++ )
48. matrix3d[i][j][k] = i+j+k+3;
49.
50. cout << "Macierz trzywymiarowa" << endl
51. << " Element srodkowy: "
52. << matrix3d[dim1/2][dim2/2][dim3/2] << endl
53. << " Powinno byc : "
54. << dim1/2 + dim2/2 + dim3/2 + 3 << endl;
55. cout << " Element ostatni : "
56. << matrix3d[dim1-1][dim2-1][dim3-1] << endl
57. << " Powinno byc : "
58. << dim1 + dim2 + dim3 << endl << endl;
59.
60. // usuwanie
61. deleteMatrix3D(matrix3d);
62.
63. // Macierze czterowymiarowe ///////////////////////////
64.
65. // alokowanie
66. int**** matrix4d = allocMatrix4D(dim1,dim2,dim3,dim4);
67.
68. // test
69. for ( int i = 0; i < dim1; i++ )
70. for ( int j = 0; j < dim2; j++ )
71. for ( int k = 0; k < dim3; k++ )
72. for ( int m = 0; m < dim4; m++ )
73. matrix4d[i][j][k][m] = i+j+k+m+4;
74.
75. cout << "Macierz czterowymiarowa" << endl
76. << " Element srodkowy: "
77. << matrix4d[dim1/2][dim2/2][dim3/2][dim4/2]
78. << endl << " Powinno byc : "
79. << dim1/2 + dim2/2 + dim3/2 + dim4/2 + 4 << endl;
80. cout << " Element ostatni : "
81. << matrix4d[dim1-1][dim2-1][dim3-1][dim4-1]
82. << endl << " Powinno byc : "
83. << dim1 + dim2 + dim3 + dim4 << endl << endl;
84.
85. // usuwanie
86. deleteMatrix4D(matrix4d);
87. }
88.
89. int** allocMatrix2D(int dim1, int dim2) {
90. int** matrix2d = new int*[dim1];
91. int* dumm = new int[dim1*dim2];
92. for ( int i = 0; i < dim1; i++ )
93. matrix2d[i] = dumm + i*dim2;
94. return matrix2d;
95. }
96.
97. void deleteMatrix2D(int**& matrix2d) {
98. delete [] matrix2d[0];
99. delete [] matrix2d;
100. matrix2d = 0;
101. }
102.
103. int*** allocMatrix3D(int dim1, int dim2, int dim3) {
104. int*** matrix3d = new int**[dim1];
105. int** dumm = new int*[dim1*dim2];
106. int* d = new int[dim1*dim2*dim3];
107. for ( int i = 0; i < dim1; i++ ) {
108. matrix3d[i] = dumm + i*dim2;
109. for ( int j = 0; j < dim2; j++ )
110. dumm[i*dim2+j] = d + (i*dim2+j)*dim3;
111. }
112. return matrix3d;
113. }
114.
115. void deleteMatrix3D(int***& matrix3d) {
116. delete [] matrix3d[0][0];
117. delete [] matrix3d[0];
118. delete [] matrix3d;
119. matrix3d = 0;
120. }
121.
122. int**** allocMatrix4D(int dim1,int dim2,int dim3,int dim4) {
123. int**** matrix4d = new int***[dim1];
124. int*** dumm = new int**[dim1*dim2];
125. int** dum = new int*[dim1*dim2*dim3];
126. int* d = new int[dim1*dim2*dim3*dim4];
127. for ( int i = 0; i < dim1; i++ ) {
128. matrix4d[i] = dumm + i*dim2;
129. for ( int j = 0; j < dim2; j++ ) {
130. dumm[i*dim2+j] = dum + (i*dim2+j)*dim3;
131. for ( int k = 0; k < dim3; k++ )
132. dum[(i*dim2+j)*dim3+k] =
133. d + ((i*dim2+j)*dim3+k)*dim4;
134. }
135. }
136. return matrix4d;
137. }
138.
139. void deleteMatrix4D(int****& matrix4d) {
140. delete [] matrix4d[0][0][0];
141. delete [] matrix4d[0][0];
142. delete [] matrix4d[0];
143. delete [] matrix4d;
144. matrix4d = 0;
145. }
Zasada tworzenia i usuwania tablic wielowymiarowych jest podobna do tej, którą omówiliśmy dla macierzy dwuwymiarowych, choć konstrukcje, jak widać, stają się szybko niepokojąco „wielopiętrowe”... Wynik tego programu to:
Macierz dwuwymiarowa
Element srodkowy: 9
Powinno byc : 9
Element ostatni : 16
Powinno byc : 16
Macierz trzywymiarowa
Element srodkowy: 16
Powinno byc : 16
Element ostatni : 28
Powinno byc : 28
Macierz czterowymiarowa
Element srodkowy: 19
Powinno byc : 19
Element ostatni : 33
Powinno byc : 33
T.R. Werner, 21 lutego 2016; 20:17