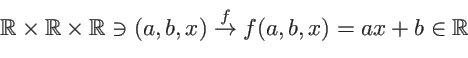2.3 Funkcje

Funkcje są podstawowym elementem programów (nie tylko w C/C++). Więcej o nich powiemy w rozdziale im poświęconym . Tu podamy tylko bardzo skrótowe wprowadzenie, by móc ich używać w dalszych przykładach.

Funkcje pełnią w programach rolę podobną do funkcji matematycznych. Definicja funkcji, jak w matematyce, jest rodzajem przepisu opisującego, jak na podstawie danych wejściowych obliczyć pewną wartość. Sama definicja nie powoduje żadnych obliczeń: po zdefiniowaniu można jednak funkcji użyć, zwykle wielokrotnie, dla różnych konkretnych wartości danych wejściowych (argumentów) — dla każdych takich konkretnych danych zostanie wtedy zastosowany przepis podany w definicji i obliczona wartość wyniku. Na przykład definicja funkcji

$\begin{displaymath} {}\mathbb{R}\times\mathbb{R}\times\mathbb{R} \ni (a,b,x) \stackrel{f}{\rightarrow} f(a,b,x) = ax+b \in \mathbb{R} \end{displaymath}$

czyli w skrócie

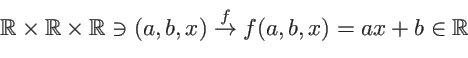
$\begin{displaymath} f(a,b,x) = ax+b \end{displaymath}$

oznacza, że za każdym razem gdy użyjemy tej funkcji, będziemy musieli podać trzy liczby rzeczywiste jako argumenty, a funkcja zwróci wynik równy iloczynowi pierwszej i trzeciej z tych liczb zwiększonemu o drugą z nich. Zauważmy, że gdy tej funkcji używamy (wywołujemy ją), to piszemy na przykład f (3, 5, w) — taki zapis oznacza zastosuj przepis podstawiając wszędzie 3 za a, 5 za b, a wartość symbolu w za x. Same nazwy a, b i x w wywołaniu funkcji nie pojawiają się. [To jest cecha C/C++; są języki, w których istnieje możliwość użycia nazw parametrów formalnych funkcji — jest to na przykład bardzo użyteczne w językach takich jak Python, Ada czy Fortran 90/95].

Podobnie jest w programowaniu. Rozważmy następujący program:

P5: funk.cpp Funkcja

      1.  #include <iostream>
      2.  using namespace std;
      3.  
      4.  double linear(double a, double b, double x) {  ➊
      5.      return a*x + b;
      6.  }
      7.  
      8.  int main() {
      9.      double c = 2, z = 3;
     10.      double result = linear(c,5,z);             ➋
     11.      cout << "Result = " << result << endl;
     12.  }

Definicja funkcji linear zaczynająca się w linii ➊ mówi tyle:

definiujemy funkcję o nazwie linear;
funkcja ta będzie potrzebować trzech liczb typu double jako danych wejściowych (argumentów). Typ double opisuje w przybliżeniu liczby rzeczywiste znane z matematyki — szerzej o tym powiemy w rozdziale o typach danych . W definicji funkcji argumenty te będą występować pod nazwami a, b i x. Jak widzimy, podobnie jak w matematyce, listę parametrów funkcji piszemy w nawiasach za nazwą tej funkcji;
typem wyniku funkcji będzie liczba rzeczywista (double) — tę informację podajemy przed nazwą funkcji;
sama definicja, za nazwą i listą parametrów, ujęta jest w nawiasy klamrowe. W naszym przypadku definicja składa się z jednej linii, ale mogłoby być ich więcej;
instrukcja return mówi, że działania funkcji tu się kończy, a jej wynikiem jest wartość wyrażenia, które pojawia się za słowem return.

W linii ➋ naszego przykładu wywołujemy funkcję linear. Jak widzimy, „posyłamy” do funkcji wartość zmiennej c (czyli 2) jako pierwszy argument, wartość 5 jako drugi, a wartośc z (czyli 3) jako trzeci. Te trzy wartości zostaną podstawione za a, b i x podczas wykonania funkcji; zwrócony przez funkcję wynik (w naszym przypadku liczba 11) będzie wartością wyrażenia ' linear(c,5,z)' i zostanie przypisany do zmiennej o nazwie result, która następnie jest wypisywana.

T.R. Werner, 21 lutego 2016; 20:17