Programowanie II R (2021/2022)

Kompilatory on-line

• http://www.onlinegdb.com/
• http://cpp.sh/
• http://www.tutorialspoint.com/compile_cpp_online.php

Ćwiczenia 17.11.2021 - klasy

1. Stwórz własną klasę Complex reprezentującą liczby zespolone
   • Zaimplementuj konstruktor
   • Zaimplementuj funkcję abs obliczającą moduł liczby
   • Zaimplementuj operator wypisywania (dodania do strumienia)
   • Zaimplementuj operator* dla dwóch liczb zespolonych
2. Napisz program do generowania bibliografii
   • Stwórz klasę Autor, która odpowiada pojedynczemu autorowi o danym imieniu, nazwisku i opcjonalnie drugiemu imieniu. Zaimplementuj wypisywanie typu: Arthur C. Clarke
   • Stwórz klasę Publikacja, która ma id (dla uproszczenia - w postaci pojedynczej cyfry od 0-9), tytuł, nazwę czasopisma, rok wydania, numer strony i listę autorów. Zaimplementuj jej wypisywanie
   • Zaimplementuj funkcję generuj, która przegląda dany tekst, a następnie wypisuje bibliografię. Publikacje na liście powinny pojawić się w takiej kolejności jak w tekście
3. Stwórz klasy Wektor i Macierz reprezentujące odpowiednio wektor długości n oraz macierz n x n (wartość n podajemy w konstruktorze).
   • zaimplementuj operator << do wypisywania do strumienia
   • zaimplementuj statyczną funkcję tworzącą przykładową macierz:
     $A = \left[ \begin{array}{cccc} 1 & 19 & 4 & 18 \\ 12 & 10 & 10 & 8 \\ 9 & 13 & 6 & 1 \\ 10 & 17 & 11 & 6 \end{array} \right]$
4. Zaimplementuj operator* dla mnożenia obu tych klas przez liczbę rzeczywistą.
5. Zaimplementuj operator* dla mnożenia przez siebie wektorów (skalarnie), macierzy (powstaje macierz) i macierzy przez wektor.
6. Zaimplementuj funkcję rozwiazU(const Macierz &U, const Wektor &y), która zwraca rozwiązanie równania $U\cdot x = y$, przy założeniu, że macierz U jest górnotrójkątna.
7. Zaimplementuj funkcję rozwiazL(const Macierz &L, const Wektor &y), która zwraca rozwiązanie równania $L\cdot x = y$, przy założeniu, że macierz L jest dolnotrójkątna.
8. Zaimplementuj funkcję rozkladLU(const Macierz &C), która zwraca macierze L i U (np. jako std::pair<Macierz,Macierz>) spełniające równanie $C=L\cdot U$, gdzie macierz U jest górnotrójkątna, a macierz L jest dolnotrójkątna.
9. Zaimplementuj funkcję rozwiaz(const Macierz &C, const Wektor &y), która zwraca rozwiązanie równania $C\cdot x = y$.
10. Zaimplementuj metodę Macierz::odwrotna(), która zwraca odwrotność macierzy C.

Ćwiczenia 24.11.2021 - kontenery STL

1. Masz dany plik tekstowy z danymi. W pliku są zapisane liczby całkowite n (mieszczące się w zakresie unsigned long long).
   • Wypisz sumę wszystkich liczb w pliku
   • Wypisz 50-tą liczbę od końca pliku
   • Wskaż, która liczba jako pierwsza się powtórzyła w pliku. Możesz założyć, że taka liczba istnieje.
2. Używając danych z poprzedniego zadania wypisz numery wierszy, które zawierają 100 największych liczb.
3. Dyskretnym logarytmem z liczby naturalnej $a$ o podstawie $b$ modulo $p$ nazywamy taką liczbę $k$, że $b^k \equiv a\ (\mathrm{mod}\ p)$. Operacja ta jest podstawą wielu algorytmów szyfrowania, gdyż obliczenie danego logarytmu jest długotrwałe, a bardzo łatwo zweryfikować, czy dana liczba $k$ jest rzeczywiście poprawnym wynikiem logarytmowania
   W tym zadaniu przyjmujemy, że liczba pierwsza p = 10006721 oraz a = 53.
   • Napisz funkcję obliczającą $k$-tą potęgę danej liczby modulo $p$ (tzw. algorytm szybkiego potęgowania)
   • Napisz funkcję obliczającą dyskretny logarytm poprzez testowanie kolejnych liczb od 0 do $p-1$ (liczby w zadaniu zostały dobrane tak, żeby $a$ było prymitywnym pierwiastkiem grupy $Z_p$, a do tego żadna z liczb z pliku nie jest podzielna przez $p$, więc ta funkcja zawsze jest dobrze zdefiniowana)
   • Dla każdej z liczb z danych z pierwszego zadania oblicz dyskretny logarytm z tej liczby modulo $p$. Wynik zapisz w kolejnych wierszach pliku wynik.txt

Ćwiczenia 01.12.2021 - klasy, c.d.

1. Zaimplementuj klasę Wielomian obslugującą następujące metody: .
   • Konstruktor umożliwiający podanie wektora współczynników wielomianu
   • Wypisywanie (przez przekierowanie do strumienia)
   • Metodę funkcyjną zwracającą wielomian x.
   • Mnożenie przez liczbę(w obie strony)
   • Mnożenie przez wielomian
   • Obliczanie pochodnej
   • Obliczenie pierwiastków (jeśli się da)
2. Zaimplementuj klasę WielomianCzebyszewa dziedziczącą po klasie wielomian. Przetestuj w szczególności wyznaczanie pierwiastków.

Ćwiczenia 08.12.2021 - klasy, c.d.

1. Rozbij kod z poprzednich zajęć na plik nagłówkowy (.h) oraz plik źródłowy (.cpp)
2. Korzystając z klas napisanych na ostatnich zajęciach napisz funkcję obliczającą sumę kwadratów pierwiastków danego wielomianu. Wykorzystaj ją do zbadania działania polimorfizmu przy przekazywaniu wielomianu przez wartość, referencję, wskaźnik
3. Napisz własny konstruktor kopiujący oraz operator przypisania. Przetestuj który z nich jest wykorzystywany w sytuacjach:
   - Wielomian w( {1,2,3} );
   - Wielomian w = Wielomian( {1,2,3} ) + 1;
4. Zmodyfikuj klasę z pierwszego zadania, żeby była wzorcem (template) pozwalającym na wygenerowanie klasy wielomianów nad danym pierścieniem (np. wielomiany o współczynnikach całkowitych, wielomiany o współczynnikach zespolonych, itp.). Następnie użyj instrukcji typedef, żeby wprowadzić "prostą" nazwę na wielomian o współrzynnikach rzeczywistych.
5. Zaimplementuj rysowanie wykresu korzystając z biblioteki matplotlib-cpp. Przydatne materiały autorstwa Krzysztofa Piaseckiego:
   Informacje wstępne dot biblioteki
   minimalny działający przykład (do skompilowania poleceniem:
   g++ mpl_test.C -o mpl_test -DWITHOUT_NUMPY -I/usr/include/python3.6m -lpython3.6m
   Zadania (w szczególności przydatne komendy w zad. 2)
   
6. Zmodyfikuj rysowanie wykresu, żeby było bardziej ogólne. Tzn. zdefiniuj czysto wirtualną klasę Funkcja, która implementuje operację obliczenia wartości. Wielomian będzie wtedy klasą pochodną.

Ćwiczenia 15.12.2021 - ciąg dalszy klas, wzorce, strumienie

1. Napisz wzorzec funkcji mid(a,b,c), która zwraca środkową z trzech wartości
2. Napisz program, który wczytuje jeden plik tekstowy i wypisuje do drugiego pliku ile razy wystąpiła która litera
3. Zaimplementuj drzewo wyszukiwań binarnych (BST)
4. Napisz program kodujący i rozkodowujący plik tekstowy wg algorytmu Huffmanna. Dla prostoty możesz "symulować" zapis binarny przez tworzenie pliku tekstowego zawierącego jedynki i zera.

Ćwiczenia 22.12.2021 - równania różniczkowe

1. Rozwiąż numerycznie równanie różniczkowe: $y' + 2y = x^3 \cdot \exp(-2 x)$ przy warunku początkowym $y(0) = 1$. Porównaj dokładność uzyskiwaną przy następujących metodach:
   • Eulera
   • midpoint
   • Rungego-Kutty 4. rzędu
   • trzykrokową metodą Adamsa-Bashfortha
2. Rozwiąż problem wahadła matematycznego $\ddot{\theta} + \frac{g}{l} \sin\theta = 0$ bez używania przybliżenia małych wychyleń. Narysuj wykres fazowy, tj. w zmiennych q,p (położenie, pęd) dla różnych warunków początkowych.

Ćwiczenia 12.01.2022

1. Zainstaluj (jeśli jeszcze nie masz) bibliotekę Boost. Jeśli instalacja się udała, kompilator będzie akceptował linię #include <boost/numeric/odeint.hpp>.
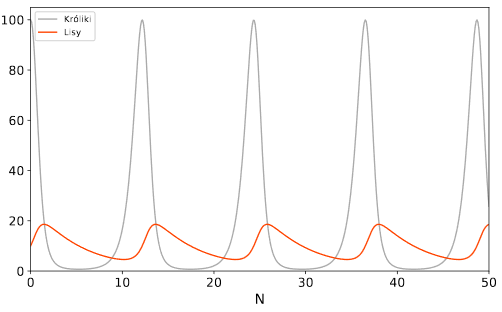
2. Bazując na przykładzie z dokumentacji biblioteki OdeInt, przeprowadź symulację populacji liczby drapieżników (np. lisów) i ich ofiar (np. królików) w danym ekosystemie. Zgodnie z równaniem Lotki-Volterry populacje te zmieniają się następująco:
   $\begin{array}{rcl} \dot{k} & = & (\alpha - \beta l) k \\ \dot{l} & = & (\delta k - \gamma) l\end{array}$
   gdzie $\alpha$ to naturalny przyrost populacji królików, $\beta$ - częstość ubywania królików wskutek polowania lisów, $\delta$ - częstość narodzin lisów, $\gamma$ - częstość ubywania lisów. Jako parametry wypróbuj wartości $\alpha =2.0$, $\beta = 0.2$, $\delta=0.01$, $\gamma = 0.2$.
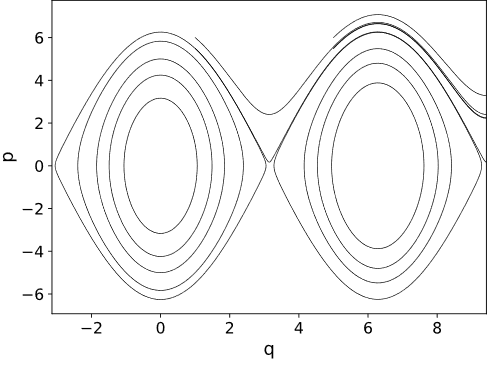
3. Korzystając z biblioteki OdeInt rozwiąż ponownie problem wahadła matematycznego $\ddot{\theta} + \frac{g}{l} \sin\theta = 0$ bez używania przybliżenia małych wychyleń. Narysuj wykres fazowy, tj. w zmiennych q,p (położenie, pęd) dla różnych warunków początkowych.
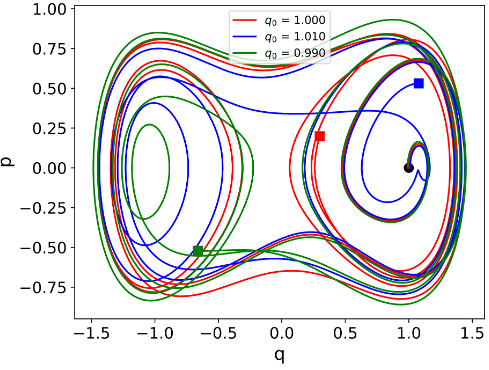
4. Oscylator Duffinga opisany jest równaniem
   $\ddot{x} + \delta \dot{x} + \beta x + \alpha x^3 = \gamma \cos(\omega t)$
   Jest to przykład dynamicznego układu przejawiającego chaotyczne zachowanie - niewielka zmiana warunków początkowych powoduje zupełnie inne zachowanie układu. Celem zadania jest wykreślenie portretu fazowego (jak w poprzednim zadaniu) takiego układu. Wypróbuj na początku parametry $\alpha=\omega=1$, $\beta = -1.0$, $\delta = 0.2$, $\gamma = 0.3$, oraz warunki początkowe $x_0 = 1.0 \pm 0.01$.
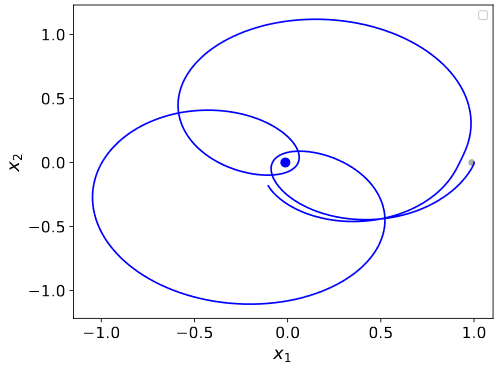
5. Rozwiąż problem ruchu sztucznego satelity umieszczonego w polu grawitacyjnym Ziemi i Księżyca. Przyjmij współrzędne $(x_1, x_2)$ opisujące położenie satelity względem środka masy (położenie Ziemi to $(-\mu,0)$, a Księżyca to $(1-\mu,0)$). Równania ruchu satelity o zaniedbywalnie małej masie względem ciał niebieskich mają wtedy następującą postać: $\begin{array}{rcl} \ddot{x_1} & = & x_1 + 2\dot{x_2} - (1-\mu)\frac{x_1+\mu}{D_1} - \mu \frac{x_1-1+\mu}{D_2}\\ \ddot{x_2} & = & x_2 - 2\dot{x_1} - (1-\mu) \frac{x_2}{D_1} - \mu \frac{x_2}{D_2} \\ D_1 & = & \left( \left(x_1 + \mu \right)^2 + x_2^2 \right)^{3/2} \\ D_2 & = & \left( \left(x_1 -1 + \mu \right)^2 + x_2^2 \right)^{3/2} \end{array}$
   gdzie parametr $\mu$ to masa Księżyca a $1-\mu$ masa Ziemi. Przyjmij $\mu = 0.01228$, a jako warunki początkowe $x_1 = 0$, $x_2 = 0$, $\dot{x_1} = 0$, $\dot{x_2} = -2$.

Ćwiczenia 19.01.2022 oraz 26.01.2022 - biblioteka Qt

1. Zainstaluj bibliotekę Qt (np. stąd) i uruchom przykładowy program.
2. Napisz prosty kalkulator (po naciśnięciu przycisku Oblicz w polu etykiety powinien pojawiać się wynik:
   
3. Stwórz następujące okienko:
   
4. Napisz program graficzny, który wyznacza pole trójkąta na podstawie podanych trzech boków (wejście i wyjście jako QLineEdit) oraz dodatkowo rysuje podany trójkąt, jeśli to możliwe
5. Napisz prosty kalkulator:
   
6. Napisz program zliczający przebieg myszki i jej średnią prędkość (w pikselach na sekundę).
7. Napisz program do badania refleksu. W tym celu utwórz widget, który w momencie uruchomienia slotu trigger() rysuje w losowym miejscu kółko o średnicy np. 20 pikseli i zaczyna mierzyć czas. Jeżeli użytkownik kliknie wewnątrz kółka, to emitowany jest sygnał correct_click(float) (argument to liczba sekund, jaka upłynęła między narysowaniem a kliknięciem), a jeśli użytkownik kliknie poza kółkiem (np. zanim kółko się pojawiło), emitowany jest sygnał wrong_click(). Po kliknięciu (niezależnie czy dobrym czy złym), widget przestaje rysować kółko i startuje QTimer o losowym czasie trwania, który znowu wywoła slot trigger().
   Oprócz tego widgetu program powinien mieć pole tekstowe do wyświetlania ostatniego wyniku oraz przycisk do włączania lub wyłączania testu.