Programowanie II R (2020/2021)

Link do zajęć: https://us02web.zoom.us/j/84380956709

Kompilatory on-line

Konta w OKWF

O kontach studenckich na Wydziale Fizyki UW można przeczytać tutaj.

Dostęp do komputerów okwf spoza Wydziału

Z zewnątrz można się połączyć tylko na jeden komputer: tempac.okwf.fuw.edu.pl. Do dostępu wykorzystuje się protokół SSH, oryginalnie przeznaczony do uruchomienia zdalnego terminala. Z komputera Linuksowego można się połączyć za pomocą polecenia ssh. Z Windows np. za pomocą Putty.

Przykład dla użytkownika ab234567, łączącego się z Linux’a, możliwość uruchamiania programów, które otwierają własne okna:

ssh -X -l ab234567 tempac.okwf.fuw.edu.pl

Dzięki odpowiednim nakładkom, protokół SSH można również wykorzystać do dostępu do plików na swoim koncie. Pod linuksem służy do tego program scp, pod Windowsem najczęściej jest wykorzystywany WinSCP.

Aby jeszcze wygodniej korzystać z plików na swoim koncie można podmontować je (lub według innej terminologii: zmapować), by były wyglądały jak pliki na lokalnym dysku. Pod linuksem efekt ten uzyskuje się przez moduł sshfs. Pod Windows należy zainstalować w tym celu dodatkowe oprogramowanie, np. podążając za tą instrukcją. Skrótowo: instalujemy WinFsp (nie mylić z przywołanym wcześniej WinScp), potem SSHFS-Win, a potem w “Mój komputer” mapujemy dysk sieciowy z adresem \\sshfs\ab234567@tempac.okwf.fuw.edu.pl gdzie w miejscu ab234567 wpisujemy nasz login.

Podczas zajęć dobrze jest pracować w katalogu o nazwie public_html, utworzonym w swoim katalogu domowym. Pliki tam umieszczone są widoczne ogólnie w Internecie, np. jeśli użytkownik ab234567 w swoim katalogu public_html ma plik program3.cpp, to można zobaczyć go wchodząc przeglądarką na adres: http://studenci.fuw.edu.pl/~ab234567/program3.cpp, co może ułatwić ewentualną pomoc.

Ćwiczenia 21.10.2020

Napisz program obliczający BMI (waga / wzrost²).
- Prawidłowe BMI mieści w zakresie 18,5-25. W zależności od wyniku program powinien wypisać stosowny komunikat (dobrze, za dużo, za mało)
Napisz program rozwiązujący równanie liniowe.
- Program powinien zapytać użytkownika o współczynniki a i b, a następnie wypisać miejsce zerowe
Napisz program rozwiązujący równanie kwadratowe
- Program powinien zapytać użytkownika o współczynniki a, b, c, a następnie wypisać wszystkie miejsca zerowe
Napisz program liczący i wyświetlający kolejne liczby Fibonacciego
- w wersji rekurencyjnej
- w wersji iteracyjnej
- porównaj szybkość wykonania z kodem napisanym w Pythonie
Napisz program liczący NWD (algorytmem Euklidesa)
Napisz program sprawdzający czy liczba jest pierwsza
Napisz program sumujący 1/kⁿ w pojedynczej i podwójnej precyzji dla n=1,2,…Nmax. Czy da się zmniejszyć liczbę mnożeń? Czy program działa wtedy dokładniej? Czy działa szybciej?

Ćwiczenia 28.10.2020

Skopiuj (a jeszcze lepiej - przepisz) poniższy fragment kodu pokazujący wykorzystanie biblioteki chrono do pomiaru odcinka czasu. Spróbuj zademonstrować następujące efekty:
- ograniczenia biblioteki chrono powodują, że nawet przy wykorzystaniu high_resolution_clock (a można też np. steady_clock) nie da się tak zmierzyć zbyt krótkich odcinków czasu, tj. dostajemy wtedy wynik po prostu 0
- czas wykonania danego fragmentu zależy również od opcji optymalizacji. Większość środowisk programistycznych posiada predefiniowane opcje kompilacji ‘Release’ i ‘Debug’. Porównaj czas działania w tych przypadkach (powinien być krótszy dla ‘Release’). Następnie usuń linijkę 20 z kodu i ponów to porównanie. Kompilator prawdopodobnie będzie wystarczająco bystry by zauważyć, że wtedy zmienna suma nie jest nam do niczego później wykorzystywana, więc w ogóle może nie robić pętli, a efekt programu (tj. co jest wypisane użytkownikowi) będzie ten sam.
```
 #include <iostream>
 #include <chrono>
 using namespace std;

 int main()
 {
     long suma = 0;
     const int NMAX = 10000000;

     // poczatek mierzenia czasu
     auto t0 = chrono::high_resolution_clock::now();

     for(int i = 0; i < NMAX; i++)
         suma += i;

     // koniec mierzenia czasu
     auto t1 = chrono::high_resolution_clock::now();
     auto dt = chrono::duration_cast<chrono::nanoseconds>(t1 - t0).count();

     cout << "Suma: " << suma << endl; // linia 20
     cout << "Czas wykonania: " << dt << " ns" << endl;
     return 0;
 }
```

Skopiuj (a jeszcze lepiej - przepisz) poniższy fragment kodu pokazujący zapis do pliku. Przetestuj jego działanie. Na tej podstawie napisz program generujący przykładowe dane do analizy. Niech program wypisuje do pliku tekstowego dwie kolumny liczb - w pierwszej kolumnie liczby od 0 do 10 z krokiem co 0.1, a w drugiej wartości odpowiadające wartościom wielomianu x²-3x+4, gdzie x jest liczbą z pierwszej kolumny. Po wszystkim użyj swojego ulubionego programu do rysowania wykresów (Gnuplot, Origin, …) do obejrzenia wyniku.

 #include <iostream>
 #include <fstream>
 using namespace std;

 int main()
 {
        
     ofstream f;                 // tworzymy strumien zwiazany z plikiem
     f.open("testowy_plik.txt"); // otwieramy plik do zapisu
        
     // w tym fragmencie mozemy uzywac tego strumienia identycznie jak cout
     f << "Hello world" << endl;
        
     f.close();                 // po wszystkim zamykamy plik

     return 0;
 }

Przećwicz definiowanie funkcji z przekazywaniem argumentów przez referencję. W tym celu:
- Napisz funkcję wypisującą na standardowe wyjście (cout) wartość n * x, gdzie x i n są argumentami funkcji (w takiej kolejności).
- Zmień sygnaturę funkcji podając domyślną wartość parametru n = 2. Sprawdź, czy możesz wtedy wywołać funkcję podając jej jeden argument (tj. x).
- Zmień funkcję tak, by zamiast standardowego wyjścia wykorzystywała strumień podany jej jako argument (funkcja będzie miała więc 3 argumenty: strumień, x, n). Zwróć uwagę, że strumień musimy przekazać jako referencję, bo chcemy by zapis był do tego samego strumienia.
W bibliotece standardowej jest funkcja pow podnosząca liczbę do zadanej potęgi. Napisz na 2 sposoby swoją konkurencyjną funkcję podnoszącą liczbę double do zadanej potęgi.
- sposobem naiwnym, tj. w pętli for mnożąc n razy daną liczbę x
- sprytniejszym sposobem tzw. potęgowania szybkiego
- porównaj szybkość działania tych trzech funkcji (Twoich dwóch i bibliotecznej) dla wykładników równych 2 oraz 10⁷.

Ćwiczenia 04.11.2020

Napisz program liczący wartość funkcji wykładniczej z dokładnością double z jej rozwinięcia w szereg.
- Porównaj wynik z funkcją exp z biblioteki cmath. Porównaj dokładność otrzymanego wyniku kiedy szereg sumowany był w kolejności 1+x+x²/2+… i w kolejności odwrotnej.
- Narysuj (w Gnuplocie/Originie/…) wykres pokazujący zbieżność tego szeregu na podstawie danych wygenerowanych przez Twój program. W pierwszej kolumnie wypisuj N, do którego sumowałeś szereg, a w drugiej różnicę między uzyskaną przez Ciebie sumą szeregu a wynikiem funkcji bibliotecznej.
Napisz program liczący sumę szeregu 1/n³. Oczekiwaną wartością jest 1.2020569031595942853997381615114499907649862923404988817922715553L. Porównaj dokładność otrzymanego wyniku kiedy szereg sumawany był wprost i w kolejności odwrotnej.
- Jak zmieni się dokładność wyniku, jeśli do obliczeń wykorzystasz typ long double.
Napisz funkcję liczącą sin(x) poprzez sumowanie szeregu x-x³/3!+x⁵/5!+… Następnie przygotuj dane do narysowania wykresu funkcji sin(x) dla x w przedziale (0, 100). Obejrzyj uzyskany wynik (w Gnuplocie/Originie/…) czy wygląda poprawnie.
Napisz program liczący funkcję dilogarytmiczną ( Li₂(x) ) na przedziale -1<x<1 z jej rozwinięcia w szereg potęgowy. Użyj tożsamości z podanego linku i napisz funkcja liczącą wartość dilogarytmu dla dowolnych rzeczywistych (wersja “z gwiazdką” – zespolonych) argumentów.
Napisz program wypisujący na standardowe wyjście (tekstowo) wszystkie diagramy Ferrersa o n-kropkach.
Napisz funkcję liczącą liczby Catalana. Dla jakiej największej liczby podaje on poprawny wynik i dlaczego zawodzi dla większych? Jak można go poprawić?
Napisz funkcję sortującą tablicę liczb o zadanym typie.

Ćwiczenia 12.11.2020

Napisz funkcję, która ma dwa argumenty: wskaźniki do kolejnych liczb Fibonacciego f_n-1 i f_n. Funkcja powinna zmienić wartości wskazywanych zmiennych na f_n-1 i f_n.
Napisz klasę reprezentującą listę podwójnie wiązaną.
Napisz klasę reprezentującą drzewo BST.

Ćwiczenia 18.11.2020

Masz dany plik tekstowy z danymi. W pliku są zapisane liczby całkowite n (mieszczące się w zakresie unsigned long long). Wskaż, która liczba jako pierwsza się powtórzyła w pliku. Możesz założyć, że taka liczba istnieje.
- Wykonaj to zadanie w dwóch wariantach: korzystając z napisanego wcześniej drzewa BST oraz z STL
Masz dany plik tekstowy z odległościami dróg między miastami w kolejnych wierszach. W każdym wierszu znajdują się kolejno dwie jednowyrazowe nazwy miast połączonych drogą, dystans w km, czas jazdy w minutach, koszt w zł oraz jednowyrazowa nazwa drogi.
- Napisz program wypisujący miasta w tej sieci drogowej
- Wypisz nazwy dróg w kolejności od najdłuższej do najkrótszej
- Wypisz nazwy płatnych dróg w kolejności od najdroższej (w sensie kosztu/km)
- Napisz program wyszukujący najkrótszą drogę między zadanymi miastami.
Napisz program znajdujący cykl Eulera w danym grafie lub stwierdzający, że takiego cyklu nie ma. Działanie przetestuj na przygotowanych przez siebie danych.
(trudniejsze) Napisz program znajdujący maksymalny przepływ w danym grafie skierowanym. Działanie przetestuj na przygotowanych przez siebie danych.

Ćwiczenia 26.11.2020

Rozwiąż numerycznie równanie różniczkowe: przy warunku początkowym . Porównaj dokładność uzyskiwaną przy następujących metodach:
- Eulera
- midpoint
- Rungego-Kutty 4. rzędu
- trzykrokową metodą Adamsa-Bashfortha
Rozwiąż problem wahadła matematycznego $\ddot{\theta} + \frac{g}{l} \sin\theta = 0$ bez używania przybliżenia małych wychyleń. Narysuj wykres fazowy, tj. w zmiennych q,p (położenie, pęd) dla różnych warunków początkowych.
Oscylator Dufflinga opisany jest równaniem $\ddot{x} + \delta \dot{x} + \alpha x + \beta x^3 = \gamma \cos{(\omega t)}$ . Jest to przykład dynamicznego układu przejawiającego chaotyczne zachowanie - niewielka zmiana warunków początkowych powoduje zupełnie inne zachowanie układu. Celem zadania jest wykreślenie portretu fazowego (jak w poprzednim zadaniu) takiego układu. Wypróbuj parametry $\alpha = \omega = 1$, $\beta = -1.0$, $\delta = 0.2$, $\gamma=0.3$ oraz warunki początkowe $x_0 = 1.0 \pm 0.01$.

Ćwiczenia 02.12.2020

Kończymy zadanie 2. sprzed dwóch tygodni zajęć. Poniżej kod wczytujący dane (jako punkt wyjścia do pisania programu)

 #include <iostream>
 #include <set>
 #include <vector>
 #include <string>
 #include <algorithm>
 #include <fstream>

 using namespace std;


 class Droga {
 public:
     string miasto1;
     string miasto2;
     double dlugosc;
     double czas;
     double koszt;
     string nazwa;

     friend istream &operator>>(istream &stream, Droga &d);
 };

 istream &operator>>(istream &stream, Droga &d) {
     stream >> d.miasto1 >> d.miasto2 >> d.dlugosc >> d.czas >> d.koszt >> d.nazwa;
     return stream;
 }

 class Miasto;

 class Polaczenie {
 public:
     Miasto * cel;
     double dlugosc;
 };

 class Miasto {
 public:
     string nazwa;
     set<Polaczenie> drogi; // drogi wychodzace z danego miasta
 };


 int main() {
     vector<Droga> drogi;

     ifstream f;
     f.open("miasta.txt");
     Droga d;
     while (f >> d) {
         drogi.push_back(d);
     }

     f.close();

     // test, czy dobrze sie wczytalo
     for(auto it = drogi.begin(); it != drogi.end(); it++)
         cout << it->nazwa << endl;

     return 0;
 }

Zainstaluj (jeśli jeszcze nie masz) bibliotekę Boost. Jeśli instalacja się udała, kompilator będzie akceptował linię #include <boost/numeric/odeint.hpp>.

Ćwiczenia 09.12.2020

Bazując na przykładzie z dokumentacji biblioteki OdeInt, przeprowadź symulację populacji liczby drapieżników (np. lisów) i ich ofiar (np. królików) w danym ekosystemie. Zgodnie z równaniem Lotki-Volterry populacje te zmieniają się następująco:
$\begin{array}{rcl} \dot{k} & = & (\alpha - \beta l) k \\ \dot{l} & = & (\delta k - \gamma) l\end{array}$
gdzie $\alpha$ to naturalny przyrost populacji królików, $\beta$ - częstość ubywania królików wskutek polowania lisów, $\delta$ - częstość narodzin lisów, $\gamma$ - częstość ubywania lisów. Jako parametry wypróbuj wartości $\alpha =2.0$, $\beta = 0.2$, $\delta=0.01$, $\gamma = 0.2$.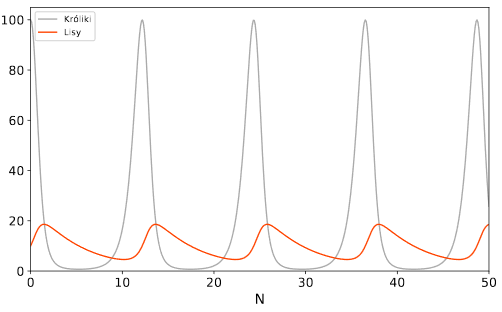
Korzystając z biblioteki OdeInt rozwiąż ponownie problem wahadła matematycznego $\ddot{\theta} + \frac{g}{l} \sin\theta = 0$ bez używania przybliżenia małych wychyleń. Narysuj wykres fazowy, tj. w zmiennych q,p (położenie, pęd) dla różnych warunków początkowych.
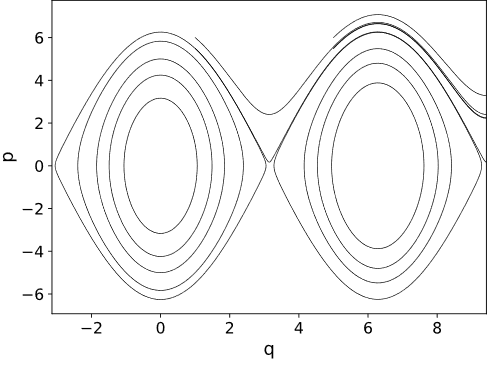
Oscylator Duffinga opisany jest równaniem
$\ddot{x} + \delta \dot{x} + \beta x + \alpha x^3 = \gamma \cos(\omega t)$
Jest to przykład dynamicznego układu przejawiającego chaotyczne zachowanie - niewielka zmiana warunków początkowych powoduje zupełnie inne zachowanie układu. Celem zadania jest wykreślenie portretu fazowego (jak w poprzednim zadaniu) takiego układu. Wypróbuj na początku parametry $\alpha=\omega=1$, $\beta = -1.0$, $\delta = 0.2$, $\gamma = 0.3$, oraz warunki początkowe $x_0 = 1.0 \pm 0.01$.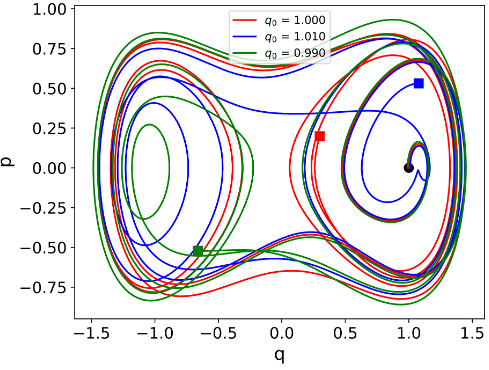
Rozwiąż problem ruchu sztucznego satelity umieszczonego w polu grawitacyjnym Ziemi i Księżyca. Przyjmij współrzędne $(x_1, x_2)$ opisujące położenie satelity względem środka masy (położenie Ziemi to $(-\mu,0)$, a Księżyca to $(1-\mu,0)$). Równania ruchu satelity o zaniedbywalnie małej masie względem ciał niebieskich mają wtedy następującą postać: $\begin{array}{rcl} \ddot{x_1} & = & x_1 + 2\dot{x_2} - (1-\mu)\frac{x_1+\mu}{D_1} - \mu \frac{x_1-1+\mu}{D_2}\\ \ddot{x_2} & = & x_2 - 2\dot{x_1} - (1-\mu) \frac{x_2}{D_1} - \mu \frac{x_2}{D_2} \\ D_1 & = & \left( \left(x_1 + \mu \right)^2 + x_2^2 \right)^{3/2} \\ D_2 & = & \left( \left(x_1 -1 + \mu \right)^2 + x_2^2 \right)^{3/2} \end{array}$
gdzie parametr $\mu$ to masa Księżyca a $1-\mu$ masa Ziemi. Przyjmij $\mu = 0.01228$, a jako warunki początkowe $x_1 = 0$, $x_2 = 0$, $\dot{x_1} = 0$, $\dot{x_2} = -2$.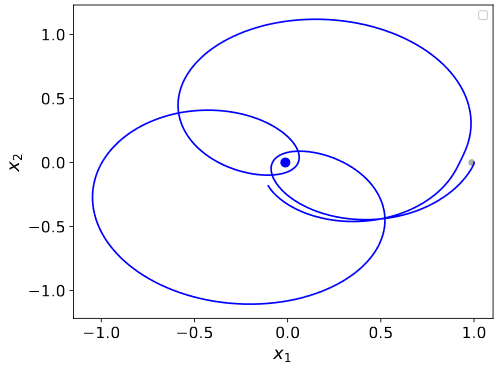

Ćwiczenia 16.12.2020 - własna implementacja algebry liniowej

Stwórz klasy Wektor i Macierz reprezentujące odpowiednio wektor długości n oraz macierz n x n (wartość n podajemy w konstruktorze).
- zaimplementuj operator << do wypisywania do strumienia
- zaimplementuj statyczną funkcję tworzącą przykładową macierz:
  $A = \left[ \begin{array}{cccc} 1 & 19 & 4 & 18 \\ 12 & 10 & 10 & 8 \\ 9 & 13 & 6 & 1 \\ 10 & 17 & 11 & 6 \end{array} \right]$
Zaimplementuj operator* dla mnożenia obu tych klas przez liczbę rzeczywistą.
Zaimplementuj operator* dla mnożenia przez siebie wektorów (skalarnie), macierzy (powstaje macierz) i macierzy przez wektor.
Zaimplementuj funkcję rozwiazU(const Macierz &U, const Wektor &y), która zwraca rozwiązanie równania $U\cdot x = y$, przy założeniu, że macierz U jest górnotrójkątna.
Zaimplementuj funkcję rozwiazL(const Macierz &L, const Wektor &y), która zwraca rozwiązanie równania $L\cdot x = y$, przy założeniu, że macierz L jest dolnotrójkątna.
Zaimplementuj funkcję rozkladLU(const Macierz &C), która zwraca macierze L i U (np. jako std::pair<Macierz,Macierz>) spełniające równanie $C=L\cdot U$, gdzie macierz U jest górnotrójkątna, a macierz L jest dolnotrójkątna.
Zaimplementuj funkcję rozwiaz(const Macierz &C, const Wektor &y), która zwraca rozwiązanie równania $C\cdot x = y$.
Zaimplementuj metodę Macierz::odwrotna(), która zwraca odwrotność macierzy C.

Ćwiczenia 08.01.2021 - własna implementacja algebry liniowej, ciąg dalszy

Można kontynuować od tego kodu.

Ćwiczenia 13.01.2021

Zaimplementuj algorytm sortowania przez scalanie (mergesort)
Zaimplementuj “wolną” transformatę Fouriera. Przetestuj ją na funkcji:
$f(x) = \left\{ \begin{array}{cc} 1 & \mathrm{gdy}\ 0.3 < x < 0.4 \\ 0 & \mathrm{w\ p.p.} \end{array} \right.$

Zaimplementuj szybką transformatę Fouriera, np. korzystając z poniższego algorytmu:

 function y = fft(f)
     N = length(f);
     if N == 1 
         y = f;
     else
         omega = exp(- 2 Pi i/ N);
		
         u = fft( f[0:2:N-2] );
         v = fft( f[1:2:N-1] );
			
         for each k:
             v[k] = v[k] * omega^k;
			
         y = [ u+v ; u-v ];
     end
 end

Użyj biblioteki FFTW do obliczenia szybkiej transformaty Fouriera. Zacznij od przykładu:

 /* Kompilacja:
     gcc -o dft dft.c -lfftw3 -lm */
 #include <complex.h> /* rozszerzenie GCC dające operacje na typach zespolonych */
 #include <fftw3.h>
 #include <math.h>
 #define N 8
	 
 int main(void)
 {
 fftw_complex *F, *C;
 fftw_plan Plan;
 double normfactor = 1.0/N;
 int i;
	 
 F = fftw_malloc( N * sizeof(fftw_complex) );
 C = fftw_malloc( N * sizeof(fftw_complex) );
	 
 for( i = 0; i < N; i++ ) /* inicjalizacja wartości tablicy F */
 {
     F[i] = i*M_PI*(1-0.5*I); 
 }
	 
 Plan = fftw_plan_dft_1d( N, F, C, FFTW_FORWARD, FFTW_ESTIMATE );
	 
 fftw_execute( Plan );
	 
 for( i = 0; i < N; i++ ) /* normalizacja wyznaczonego C */
     C[i] *= normfactor; 
	 
 for( i = 0; i < N; i++ )
 {
     printf("F[%d] = %8.3lf + %8.3lfi | C[%d] = %8.3lf + %8.3lfi\n", 
     i, creal(F[i]), cimag(F[i]), i, creal(C[i]), cimag(C[i])); 
 }
	 
 /* .... teraz moglibyśmy zmienić wartości F i ponownie wyznaczyć C,
 korzystając z tego samego Planu! */
	 
 /* sprzątamy */
	 
 fftw_destroy_plan( Plan );
 fftw_free( F ); 
 fftw_free( C ); 
	 
 return(0);
 }

Porównaj szybkość działania tych implementacji.
Wykorzystaj bibliotekę Eigen do wyznaczenia rozkładu LU. Korzystając z tej biblioteki oblicz wektory własne i wartości własne macierzy A z zajęć 16.12.2020.

Ćwiczenia 20.01.2021 - biblioteka Qt

Zainstaluj bibliotekę Qt (np. stąd) i uruchom przykładowy program.
Stwórz następujące okienko:
Napisz program graficzny, który wyznacza pole trójkąta na podstawie podanych trzech boków (wejście i wyjście jako QLineEdit) oraz dodatkowo rysuje podany trójkąt, jeśli to możliwe
Napisz prosty kalkulator:
Napisz program zliczający przebieg myszki i jej średnią prędkość (w pikselach na sekundę).
Napisz program do badania refleksu. W tym celu utwórz widget, który w momencie uruchomienia slotu trigger() rysuje w losowym miejscu kółko o średnicy np. 20 pikseli i zaczyna mierzyć czas. Jeżeli użytkownik kliknie wewnątrz kółka, to emitowany jest sygnał correct_click(float) (argument to liczba sekund, jaka upłynęła między narysowaniem a kliknięciem), a jeśli użytkownik kliknie poza kółkiem (np. zanim kółko się pojawiło), emitowany jest sygnał wrong_click(). Po kliknięciu (niezależnie czy dobrym czy złym), widget przestaje rysować kółko i startuje QTimer o losowym czasie trwania, który znowu wywoła slot trigger().
Oprócz tego widgetu program powinien mieć pole tekstowe do wyświetlania ostatniego wyniku oraz przycisk do włączania lub wyłączania testu.