Narzędzia obliczeniowe w analizie danych eksperymentalnych fizyki materii skondensowanej (2022/2023)

Materiały pomocnicze

• Origin, cz. 1 - w spakowanym pliku znajdują się dane oraz wzorcowe wykresy.
• Origin, cz. 2 - w spakowanym pliku znajdują się dane oraz wzorcowe wykresy.
• Pleview, cz. 1 (plik zip z programem)
• Pleview, cz. 2 - kolokwium z 2018 r.
• Pleview, cz. 3 - kolokwium z 2019 r., zad. dodatkowe
• Python - kurs Programowanie I R
• Python - ćwiczenia w3resource
• Zajęcia 01.12.2022
  
  1. Wróć do przykładowych wykresów "Origin, cz. 1" i wykonaj z wykorzystaniem Matplotlib zadania: 1, 2, 4
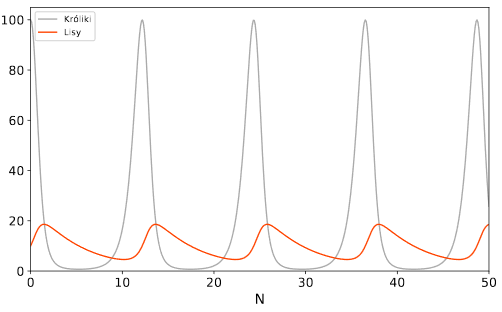
  2. Przeprowadź symulację populacji liczby drapieżników (np. lisów) i ich ofiar (np. królików) w danym ekosystemie. Zgodnie z równaniem Lotki-Volterry populacje te zmieniają się następująco:
     $\begin{array}{rcl} \dot{k} & = & (\alpha - \beta l) k \\ \dot{l} & = & (\delta k - \gamma) l\end{array}$
     gdzie $\alpha$ to naturalny przyrost populacji królików, $\beta$ - częstość ubywania królików wskutek polowania lisów, $\delta$ - częstość narodzin lisów, $\gamma$ - częstość ubywania lisów. Jako parametry wypróbuj wartości $\alpha =2.0$, $\beta = 0.2$, $\delta=0.01$, $\gamma = 0.2$.
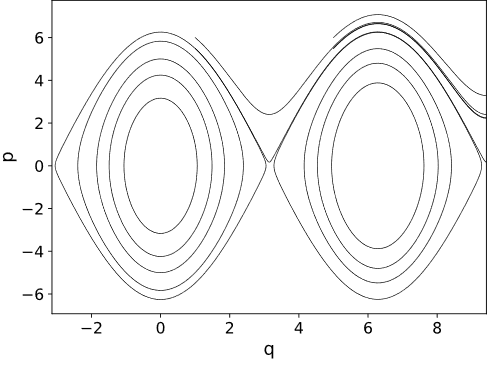
  3. Rozwiąż problem wahadła matematycznego $\ddot{\theta} + \frac{g}{l} \sin\theta = 0$ bez używania przybliżenia małych wychyleń. Narysuj wykres fazowy, tj. w zmiennych q,p (położenie, pęd) dla różnych warunków początkowych.
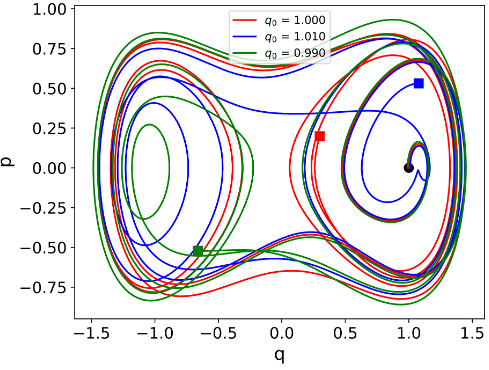
  4. Oscylator Duffinga opisany jest równaniem
     $\ddot{x} + \delta \dot{x} + \beta x + \alpha x^3 = \gamma \cos(\omega t)$
     Jest to przykład dynamicznego układu przejawiającego chaotyczne zachowanie - niewielka zmiana warunków początkowych powoduje zupełnie inne zachowanie układu. Celem zadania jest wykreślenie portretu fazowego (jak w poprzednim zadaniu) takiego układu. Wypróbuj na początku parametry $\alpha=\omega=1$, $\beta = -1.0$, $\delta = 0.2$, $\gamma = 0.3$, oraz warunki początkowe $x_0 = 1.0 \pm 0.01$.
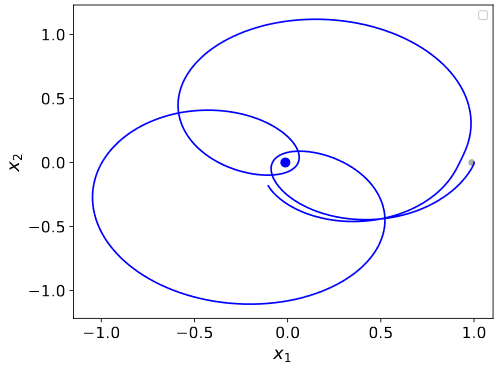
  5. Rozwiąż problem ruchu sztucznego satelity umieszczonego w polu grawitacyjnym Ziemi i Księżyca. Przyjmij współrzędne $(x_1, x_2)$ opisujące położenie satelity względem środka masy (położenie Ziemi to $(-\mu,0)$, a Księżyca to $(1-\mu,0)$). Równania ruchu satelity o zaniedbywalnie małej masie względem ciał niebieskich mają wtedy następującą postać: $\begin{array}{rcl} \ddot{x_1} & = & x_1 + 2\dot{x_2} - (1-\mu)\frac{x_1+\mu}{D_1} - \mu \frac{x_1-1+\mu}{D_2}\\ \ddot{x_2} & = & x_2 - 2\dot{x_1} - (1-\mu) \frac{x_2}{D_1} - \mu \frac{x_2}{D_2} \\ D_1 & = & \left( \left(x_1 + \mu \right)^2 + x_2^2 \right)^{3/2} \\ D_2 & = & \left( \left(x_1 -1 + \mu \right)^2 + x_2^2 \right)^{3/2} \end{array}$
     gdzie parametr $\mu$ to masa Księżyca a $1-\mu$ masa Ziemi. Przyjmij $\mu = 0.01228$, a jako warunki początkowe $x_1 = 1$, $x_2 = 0$, $\dot{x_1} = 0$, $\dot{x_2} = -2$.
• W pliku spadanie.dat są dane (czas, położenie) spadku pewnego obiektu. Załóż, że równanie ruchu ma postać: $a = - g + \alpha v^2$, tzn. że opory ruchu są proporcjonalne do kwadratu prędkości. Dopasuj wartości parametrów $g$ i $\alpha$.
• Python - kolokwium z 2021 r.
• Python - symulacja precesji spinu jonu manganu