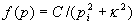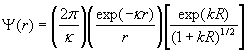Halo Nuclei

The apparent reason for the formation of a neutron halo is simple and can be understood in terms of a potential model. Let us assume that a nucleus has a neutron loosely bound to an inert core. We further introduce the simplification that the interaction potential between the neutron and the core is a square well, the size of which is that of the core nucleus itself. The wavefunction of the neutron outside the potential is written as where R is the width of the potential. 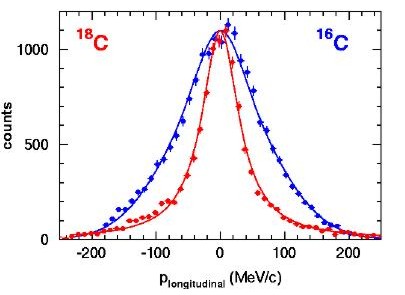Using this wavefunction, the density distribution of the neutron is written as The size is reflected in large nucleon removal cross sections and narrow momentum distributions. Since tunnelling is a purely quantum mechanical phenomenon, the halo has no classical analogy [1]. The parameter k, which determines the slope of density tail, is related to a separation energy of the neutron (ES) by where μ is the effective mass of the system. As can be seen from these equations, when Es decreases κ becomes smaller and thus, the tail of the distribution becomes longer. 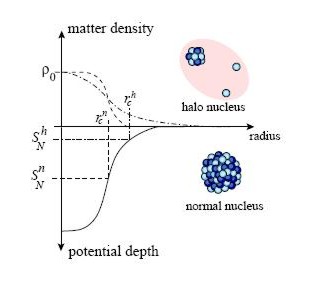Although the surface diffuseness is known to be equal for all stable nuclei, that constancy is now understood simply as a reflection of the nearly-constant nucleon separation energy (6-8 MeV) for stable nuclei. In fact, the asymptotic slope of the density distribution of stable nuclei is consistent with the slope calculated by above mentioned equation. In general, the surface diffuseness is expected to depend on the nucleon separation energy. The neutron halo is the most pronounced case for a small separation energy (< 1 MeV). The momentum distribution [f(pi)] of the neutron is expressed by the Fourier transform of the wavefunction where pi is the Cartesian component of the momentum. The width of the momentum distribution is again related to parameter κ. In contrast with the density distribution, the smaller the Es, the smaller the width of the distribution. This is obviously a reflection of Heisenberg's uncertainty principle: when the distribution in coordinate space is wide, that in momentum space is narrow[2]. 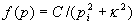[1] K. Markenroth, Exploring the Exotic: Experimental investigations far from stability,Department of Experimental Physics Chalmers University of Technologyand Göteborg University Göteborg, Sweden, 2001 [2] I.Tanihata, Neutron halo nuclei, J. Phys. G: Nucl. Part. Phys. 22 (1996) 157-198. Printed in the UK