Fale de Broglie’a – Bohma w
nanoelektronice
Janina
Marciak-Kozłowska
Mirosław
Kozłowski
Instytut
Technologii Elektronowej, Al. Lotników 32/46, 02-668 Warszawa
Streszczenie
W opracowaniu przedstawiono perspektywy wykorzystania fal materii (fal de Broglie’a) w nanoelektronice. Wskazano na możliwości wykorzystania fal materii w elementach elektronicznych ze szczególnym uwzględnieniem „kwantowych stadionów” (quantum stadium, corrals). Opracowanie jest rozszerzoną wersją projektu badawczego: „Fizyczne podstawy dynamiki fal materii w nanostrukturach” złożonego do KBN w 2004 r.
Słowa kluczowe:
Fale materii, kwantowe stadiony, impedancja i rezystancja fal materii.
Spis
treści
2... Podstawowe własności nanostruktur
3... Technologiczne aspekty fal de Broglie’a.
Równoważność jednocząstkowych stacjonarnych fal de Broglie’a i fal świetlnych
Porównanie własności fal de Broglie’a – Bohma i fal elektromagnetycznych
Siły, moc, impedancja w ruchu harmonicznym (struna)
De Broglie-Bohm waves in nanoelectronics
Abstract
In recent years, the advances in
scanning tunneling microscopy (STM) made possible the manipulation of single
atoms on top of a surface and the construction of quantum structure of
arbitrary shape. In particular, stadium type quantum corrals have been
assembled by depositing a close line of atoms on Cu or noble metal. In this
paper the quantum structure of the atomic corrals is discussed. The operation
of quantum corrals was described as being similar to light waves.
Key words: Matter waves; Quantum stadium;
Quantum corral; impedance; conductance.
Contents
1. Introduction............................................................................................................................ 5
2. The operation of nanostructures............................................................................................... 7
3. Technology of the matter (de
Broglie-Bohm waves)............................................................... 12
4. Impedance of the matter waves............................................................................................. 13
5. Reference............................................................................................................................. 15
Appendix A................................................................................................................................ 16
Comparison of matter and light waves
Appendix B................................................................................................................................ 17
Comparison of de Broglie and electromagnetic waves
Appendix C................................................................................................................................ 18
Forces, power and impedance of the harmonic motion
1. Wstęp
Od kilku lat badane są możliwości przekazywania informacji na poziomie atomowym za pomocą struktur elektronowych – „stadionów kwantowych” (quantum stadium, corrals). Chodzi tu o prace prowadzone przede wszystkim w Almaden Research Center (IBM) pod kierunkiem D. M. Eiglera*. Struktury typu quantum studium (quantum corrals) są wspaniałym wspólnym rezultatem technologii i badań podstawowych. Powstają one, atom po atomie (zwykle 30–80 atomów) umieszczonych za pomocą STM (scanning tunneling) na powierzchni metalu. Zwykle mają one kształt elipsy o dużej osi rzędu 10 nm. Własności struktur bada się za pomocą STM. Uzyskany obraz w STM odpowiada stojącym falom elektronów de Broglie’a – Bohma. W pracach grupy D. M. Eiglera wykazano możliwość przekazywania informacji w gazie elektronowym zamkniętym w „kwantowym stadionie” (quantum stadium, corrals). Umieszczając dodatkowy atom w jednym z ognisk elipsy uzyskuje się jego obraz – miraż (quantum mirage) w drugim ognisku elipsy. Rozwój technologii uzyskiwania kwantowych miraży stanowi podstawę poszukiwań nowych elementów elektronicznych w skali atomowej.
Nośnikiem informacji w „kwantowych stadionach” są fale materii – fale de Broglie’a.
Fale materii – fale de Broglie’a-Bohma stanowią jedną z
realizacji potencjalności cząstek materialnych: elektronów, nukleonów,
jąder atomowych i cząsteczek. W ortodoksyjnej (kopenhaskiej) interpretacji
mechaniki kwantowej wynik pomiaru wybranej własności cząsteczki, na przykład
jej położenia, traktuje się jako rezultat uśrednienia po ensamblu pomiarów.
W związku z rozwojem technologii elektronowej, a w
szczególności nanotechnologii, podejście probabilistyczne (interpretacja
kopenhaska) musi zostać poddane rewizji. W nanotechnologii mamy do
czynienia ze strukturami jednocząsteczkowymi, lub ostatnio jednoatomowymi, w
których możemy dokonać pomiaru własności elektrycznych oraz cieplnych
nanostruktur.
Nanostruktury stanowią front badań w dziedzinie technologii
i fizyki ciała stałego. Rozmiary nanostruktur są większe od rozmiarów molekuł i
mniejsze od mikrostruktur używanych w standardowej technologii elektronowej.
Ponieważ nanostruktury zawierają zwykle kilkanaście do kilkudziesięciu atomów,
stanowią naturalny przedmiot badania i rozwoju inżynierii atomowej.
Własności nanostruktur z jednej strony odpowiadają dużym obiektom kwantowym a z
drugiej, ze względu na bardzo małe rozmiary nanostruktur (![]() ), różnią się istotnie od własności struktur mikroskopowych (
), różnią się istotnie od własności struktur mikroskopowych (![]() ).
).
Mikrostruktury, choć bardzo małe w porównaniu ze strukturami
makroskopowymi, można budować i badać za pomocą metod technologii makroskopowej
opartej na fizyce klasycznej. Natomiast technologia nanostruktur oparta jest na
fizyce kwantowej. Stąd nanostruktury są nowym stanem materii o wyjątkowym znaczeniu
dla przyszłego rozwoju technologii i nauki.
Ze względu na bardzo małe rozmiary, nanostruktury mogą być
bardzo gęsto upakowane w elementach elektronicznych. Dzięki temu, można
spodziewać się znacznego zwiększenia szybkości transferu informacji w
elementach elektronicznych i większej pamięci tych elementów.
Na początku trzeciego tysiąclecia możemy mówić o powstaniu
nowej dyscypliny naukowej – nanoscience, która łączy w sobie metody
badawcze fizyki, chemii, biologii i elektroniki. W dziedzinie fizyki i
chemii nanoscience prowadzi do rozwoju metod badawczych dotyczących np.
szybkości reakcji chemicznych przebiegających na poziomie atomowym i
molekularnym (prace A. Zewail [1]). W biologii molekularnej nanostruktury
stanowią podstawowe składniki komórek. W tej dziedzinie szczególnie
interesujące są wyniki Hameroffa i R. Penrose’a [2] dotyczące nanotubul
– składników neuronów. W nanoelektronice badane są własności elektryczne
wybranych molekuł jako przyszłych elementów elektronicznych.
2. Podstawowe własności nanostruktur
Pojedyncza nanostruktura wyróżnia się własnościami, które
możemy podzielić na dwie grupy. Do pierwszej grupy zaliczamy zależność
własności nanostruktury od jej geometrycznych rozmiarów. Kolor „złotej”
nanostruktury zawierającej kilkadziesiąt atomów złota Au zmienia się w
zależności od liczby atomów. Do drugiej grupy należą własności nanostruktur
związane z obecnością defektów i jakością powierzchni nanostruktur. Przy tym
jakość powierzchni nanostruktury i jej wpływ na własności fizyczne
nanostruktury jest znacznie większy niż ma to miejsce w przypadku
makrostruktur.
Układy nanostruktur – assemblery wykazują własności,
które w istotny sposób zależą od natury oddziaływania między poszczególnymi
nanostrukturami. Oddziaływania elektromagnetyczne między nanostrukturami,
tunelowanie, zjawiska transportu wewnątrz assemblera wpływają na własności
elementów elektronicznych.
W dziedzinie budowy układów elektronicznych zawierających
nanostruktury szczególną rolę odgrywa elektronika
molekularna.
Duże nadzieje wiążemy z cząsteczkami organicznymi jako przyszłymi układami
elektronicznymi. Własności elektryczne układów metal – cząsteczka organiczna –
metal, a w szczególności ich charakterystyki IV wskazują na możliwości
konstruowania powtarzalnych stabilnych nanostruktur jako przyszłych elementów
elektronicznych w zakresie napięć – 0.1 V ® 1 V. Dla napięć większych 1.2 V złącze metal – cząsteczka
organiczna – metal traci stabilność [3].
Na rys. 1 przedstawiono piramidę złożoną z atomów
germanu na podłożu krzemowym. Rozmiary piramidy: długość podstawy 10 nm i
wysokość 1.5 nm. Powstanie piramidy – assemblera germanowego jest
procesem spontanicznym. W kilka sekund po nałożeniu atomów germanu na podłożu
krzemowym oddziaływanie między atomami germanu spontanicznie kreuje piramidę.
Powstanie piramidy stanowi przykład przyszłych technologii elektronowych, w
których wybrane struktury będą powstawały spontanicznie w milionach egzemplarzy
jednocześnie.
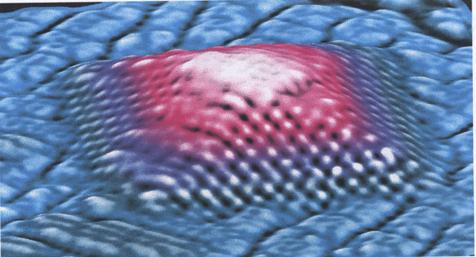
Rys. 1: Piramida złożona z atomów
germanu na podłożu krzemowym
(Hewlett-Packard,
Science Report, 1999)
Na rys. 2 przedstawiono obraz z STM tak zwanego
„kwantowego stadionu”. Stadion powstał w wyniku nałożenia 48 atomów żelaza
na podłożu z czystej miedzi. Atomy żelaza rozmieszczono za pomocą ostrza
mikroskopu tunelowego. Na powierzchni miedzi znajdują się swobodne elektrony
tworzące dwuwymiarowy gaz elektronowy. Atomy „stadionu” ograniczają ruch
elektronów. Oddziaływanie elektronów ze ścianą stadionu jest zjawiskiem
kwantowym. W obrazie kwantowym z każdym elektronem związana jest fala de Broglie’a
o długości ![]() , gdzie
, gdzie ![]() jest stałą Plancka, a p
oznacza pęd elektronu. Interferencja fal elektronowych prowadzi do powstania
periodycznej struktury określającej prawdopodobieństwo znalezienia elektronu w
wybranym położeniu.
jest stałą Plancka, a p
oznacza pęd elektronu. Interferencja fal elektronowych prowadzi do powstania
periodycznej struktury określającej prawdopodobieństwo znalezienia elektronu w
wybranym położeniu.

Rys. 2: „Stadion” (quantum stadium, corral) zbudowany z
atomów żelaza na podłożu miedziowym. Widoczna struktura interferencyjna fal
elektronowych (Surface Rev. Lett. 3 (1995) p. 127)
Dzięki zastosowaniu STM z przewodzącym ostrzem można badać
elektronową strukturę powierzchni materiałów elektronicznych. W pracy [4]
uzyskano mikroskopowy obraz (STM) powierzchni Cu na której umieszczono 30
atomów Co. Atomy utworzyły elipsę o rozmiarach: duża oś a = 7.1 nm,
mimośród e = 0.5. Po umieszczeniu dodatkowego atomu Co w
ognisku elipsy (rys. 3) uzyskano kwantowy miraż atomu Co w drugim ognisku
elipsy. Stwarza to nowe możliwości spektroskopii atomowej „na odległość”
(spectroscopy at a distance). Występowanie miraży kwantowych pozwoli w przyszłości
przekazywać informacje o stanach elektronów za pomocą fal elektronowych.
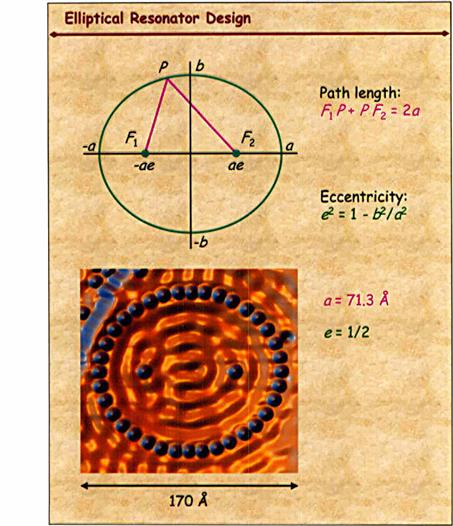
Rys. 3: Miraż kwantowy (rezonator eliptyczny),
N.C. Manoharan et al., Nature 403 (2000) p. 512.
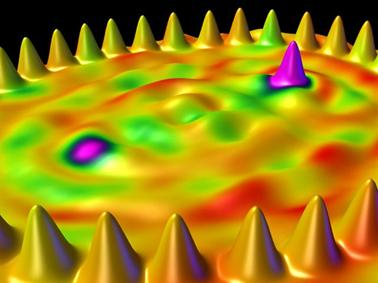
Rys. 4. Miraż kwantowy.
Wewnątrz stadionu z 30 atomów Co umieszczono dodatkowy atom Co w ognisku stadionu
– elipsy. Rozmiary elipsy: duża oś = 7.13 nm, mimośród e = 0.786 (N.C. Manoharan et al., Nature 403, (2000) p. 512)
d) b) c) a)

Rys. 5. Miraż kwantowy. (5a) Dodatkowy atom Co
umieszczony w ognisku elipsy a = 7.1 Å, e=0.786; (5b)
Dobrze widoczny obraz atomu w drugim ognisku; (5c) Dodatkowy atom
umieszczony poza ogniskiem elipsy (5d) Brak obrazu atomu. (N.C.
Manoharan et al., Nature (2000) p. 512, IBM Research
Division, Almaden Research Center, California 95120, USA)
3. Technologiczne aspekty fal de Broglie’a.
Rozwój nanotechnologii wymaga nowego technologicznego
podejścia do kwantowych własności elektronów. Przeniesienie takich podstawowych
pojęć technologicznych jak opór elementu elektronicznego, impedancja,
rezystancja, na grunt nanostruktur wymaga nowego odczytania własności
rozwiązań równania Schödingera – funkcji falowych. Stanowi to dość
skomplikowane zagadnienie biorąc choćby po uwagę złożoność klasycznego opisu
przepływu energii w ruchu falowym. Rozważmy na przykład impedancję fal Z,
poruszających się w próżni (bez rozproszeń). Maxwellowska fala
elektromagnetyczna poruszająca się w próżni natrafia na impedancję 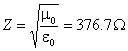 [5], gdzie
[5], gdzie ![]() i
i ![]() są odpowiednio
przenikalnością elektryczną (permittivity) oraz przenikalnością magnetyczną
(permeability) próżni.
są odpowiednio
przenikalnością elektryczną (permittivity) oraz przenikalnością magnetyczną
(permeability) próżni.
Z kolei w klasycznym opisie oporu przewodnika zderzenia
nośników ładunku, elektronów, z siecią krystaliczną określają wartość
przewodnictwa. Przy braku zderzeń przewodnictwo dąży do nieskończoności.
W standardowej mechanice kwantowej każdy układ (atom,
cząsteczka) jest reprezentowany przez funkcję falową ![]() [6]. Funkcja falowa
[6]. Funkcja falowa ![]() była opisywana jako
wielkość zespolona, która przedstawia amplitudę prawdopodobieństwa dla układu i
nie jest fizycznie mierzalna. Począwszy od prac H. C. Manoharana i
D. M. Eiglera [4] oraz E. J. Hellera [5]
możemy „obserwować” kształt stojących fal elektronowych.
była opisywana jako
wielkość zespolona, która przedstawia amplitudę prawdopodobieństwa dla układu i
nie jest fizycznie mierzalna. Począwszy od prac H. C. Manoharana i
D. M. Eiglera [4] oraz E. J. Hellera [5]
możemy „obserwować” kształt stojących fal elektronowych.
W dziedzinie nanotechnologii kwantowe procesy tunelowania
fal materii [6, 7], są praktyczną konsekwencją kwantowych własności
elektronowych fal materii. Funkcja falowa swobodnego elektronu ![]() ma postać
ma postać
![]() (1)
(1)
Wzór (1) zawiera całą informację o ruchu elektronu i jego energii.
Mechanika kwantowa zawiera nowy, w porównaniu do fizyki
klasycznej, obraz materii [6, 7]. Własności składników materii w opisie
kwantowym są nie do końca zdefiniowanymi potencjalnościami, których
ewolucja zależy od oddziaływania składnika z otoczeniem oraz od samego
składnika materii. Rozpatrzmy jako przykład elektron o określonym
pędzie ![]() , a zatem reprezentowany przez fale de Broglie’a o
długości
, a zatem reprezentowany przez fale de Broglie’a o
długości ![]() . W oddziaływaniu z siecią krystaliczną metalu elektron
zachowuje się jak fala. Ten sam elektron zachowuje się jak cząstka w
oddziaływaniu z kliszą fotograficzną, na której ślad elektronu wyznacza jego
położenie. W doświadczeniu Younga, oddziaływanie elektronu z dwoma szczelinami,
elektron w sposób ciągły przedstawia obie potencjalności – najpierw jako
fala oddziałująca z dwoma szczelinami jednocześnie,
a następnie zostawiając ślad na kliszy (cząstka). Stąd wniosek, że rodzaj
aparatu pomiarowego, z którym elektron oddziałuje determinuje, która potencjalność elektronu pęd albo położenie
zostanie zrealizowana. Pełną wiedzę o potencjalnościach elektronu
zawiera funkcja falowa
. W oddziaływaniu z siecią krystaliczną metalu elektron
zachowuje się jak fala. Ten sam elektron zachowuje się jak cząstka w
oddziaływaniu z kliszą fotograficzną, na której ślad elektronu wyznacza jego
położenie. W doświadczeniu Younga, oddziaływanie elektronu z dwoma szczelinami,
elektron w sposób ciągły przedstawia obie potencjalności – najpierw jako
fala oddziałująca z dwoma szczelinami jednocześnie,
a następnie zostawiając ślad na kliszy (cząstka). Stąd wniosek, że rodzaj
aparatu pomiarowego, z którym elektron oddziałuje determinuje, która potencjalność elektronu pęd albo położenie
zostanie zrealizowana. Pełną wiedzę o potencjalnościach elektronu
zawiera funkcja falowa ![]() będąca rozwiązaniem
równania Schrödingera.
będąca rozwiązaniem
równania Schrödingera.
![]() (2)
(2)
Przy tym, zanim elektron zacznie oddziaływać z detektorem,
funkcja falowa ![]() zawiera informacje
o prawdopodobieństwie położenia elektronu i o prawdopodobieństwie jego
pędu
zawiera informacje
o prawdopodobieństwie położenia elektronu i o prawdopodobieństwie jego
pędu ![]() . Ale funkcja falowa nie podaje, która z tych potencjalności
zostanie zrealizowana w oddziaływaniu elektronu z aparatem pomiarowym.
Dopiero specyfikacja detektora, który może mierzyć albo położenie albo pęd
elektronu (ale nie jednocześnie) umożliwia stwierdzenie, która z potencjalności zostanie zaobserwowana.
. Ale funkcja falowa nie podaje, która z tych potencjalności
zostanie zrealizowana w oddziaływaniu elektronu z aparatem pomiarowym.
Dopiero specyfikacja detektora, który może mierzyć albo położenie albo pęd
elektronu (ale nie jednocześnie) umożliwia stwierdzenie, która z potencjalności zostanie zaobserwowana.
Na podstawie powyższych rozważań dochodzimy do podstawowego
twierdzenia mechaniki kwantowej: własności falowe materii są tak samo realne
jak jej własności korpuskularne. W omawianej „zagrodzie” atomowej nie znamy
położenia elektronu wewnątrz zagrody, dlatego elektrony demonstrują swoją potencjalność falową: obraz
interferencyjny.
4. Impedancja fal materii
Impedancja i rezystancja fal elektromagnetycznych są
podstawowymi parametrami technologicznymi dla makroskopowych układów
elektronicznych pracujących w dziedzinie zbierania i przekazu informacji. W nanotechnologii
odpowiednikiem fal elektromagnetycznych na poziomie atomowym są fale de
Broglie’a. Znajomość parametrów: kwantowej impedancji i rezystancji
umożliwi sformułowanie technologicznych metod analizy atomowych układów
elektronicznych.
W kwantowym opisie rezystancji i impedancji nanostruktur
korzystamy z transformaty Fouriera funkcji falowej:
![]() . (3)
. (3)
Funkcja falowa ![]() opisuje stan kwantowy
elektronu o energii
opisuje stan kwantowy
elektronu o energii ![]() poruszającego się
z wektorem falowym
poruszającego się
z wektorem falowym ![]() . Elektrony o dużej energii
. Elektrony o dużej energii ![]() , ale składające się na prąd o małym natężeniu wykazują dużą
impedancję i vice versa. Występujący we wzorze (2) Hamiltonian H
decyduje o wartości impedancji i rezystancji, ponieważ opisuje on ewolucję w
czasie układu kwantowego [1].
, ale składające się na prąd o małym natężeniu wykazują dużą
impedancję i vice versa. Występujący we wzorze (2) Hamiltonian H
decyduje o wartości impedancji i rezystancji, ponieważ opisuje on ewolucję w
czasie układu kwantowego [1].
Ogólny wzór na
impedancję kwantową Z zapisujemy w postaci
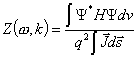 . (4)
. (4)
We wzorze (4) q jest ładunkiem nośnika prądu, ![]() gęstością prądu, dv
– oznacza element objętości a
gęstością prądu, dv
– oznacza element objętości a ![]() element powierzchni,
przez którą płynie prąd J.
element powierzchni,
przez którą płynie prąd J.
![]() . (5)
. (5)
Korzystając z wzorów
(2–4) należy: (a) rozwiązać równanie Schrödingera (2), (b) wstawić funkcję
falową ![]() do równania (4) i
wyznaczyć impedancję oraz konduktancję
do równania (4) i
wyznaczyć impedancję oraz konduktancję
![]()
Znajomość impedancji
Z i konduktancji G pozwala oszacować moc absorbowaną ![]() w nanostrukturze.
w nanostrukturze.
![]() (6)
(6)
W przypadku układu
dwóch nanostruktur o impedancjach Z1 i Z2,
warunek dopasowania nanostruktur (brak odbitych fal de Broglie’a) ma postać:
![]() (7)
(7)
Z kolei, gdy na granicy nanostruktur warunek dopasowania
nie jest spełniony
![]() (8)
(8)
wówczas
![]() (9)
(9)
gdzie R oznacza współczynnik odbicia fal de
Broglie’a
![]() (10)
(10)
a T jest współczynnikiem transmisji fal de Broglie’a
![]() (11)
(11)
Współczynniki R
i T określają podstawowe własności transmisyjne nanostruktur na poziomie
atomowym.
W uzupełnieniach A, B,
C przedstawiono zagadnienia związane z równoważnością własności fal materii i
fal elektromagnetycznych. W uzupełnieniu A przedstawiono dyskusję własności
jednocząstkowych fal de Broglie’a i fal świetlnych. Oba rodzaje fal: fale de
Broglie’a cząstek materialnych ![]() i fotonów
i fotonów ![]() spełniają identyczne
równanie falowe – równanie Helmholtza. Należy jednak pamiętać, że dotyczy to
tylko układów jednocząstkowych. W przypadku układów wielocząstkowych
stacjonarne funkcje Greena dla fal materii i fal fotonów spełniają różne
równania falowe [A1]. W uzupełnieniu B przedstawiono podstawowe informacje
dotyczące teoretycznego opisu fal materii i fal elektromagnetycznych.
W szczególności omówiono takie pojęcia jak amplituda fali,
prawdopodobieństwo znalezienia cząstki w wybranym położeniu oraz prąd
prawdopodobieństwa. Uzupełnienie C zawiera dyskusję pojęcia impedancji dla fal
elektromagnetycznych (fotonów).
spełniają identyczne
równanie falowe – równanie Helmholtza. Należy jednak pamiętać, że dotyczy to
tylko układów jednocząstkowych. W przypadku układów wielocząstkowych
stacjonarne funkcje Greena dla fal materii i fal fotonów spełniają różne
równania falowe [A1]. W uzupełnieniu B przedstawiono podstawowe informacje
dotyczące teoretycznego opisu fal materii i fal elektromagnetycznych.
W szczególności omówiono takie pojęcia jak amplituda fali,
prawdopodobieństwo znalezienia cząstki w wybranym położeniu oraz prąd
prawdopodobieństwa. Uzupełnienie C zawiera dyskusję pojęcia impedancji dla fal
elektromagnetycznych (fotonów).
5. Literatura cytowana
[1]
H. Zewail, J. Phys. Chem. A104, (2000), p. 5660.
[2]
R. Hameroff and R. Penrose, Journal
of Consciousness Studies 3, (1966), p. 36.
[3]
J. Reichert at al., Phys. Rev.
Lett. 88, (2002), p. 176804.
[4]
N. C. Manoharan et al., Nature,
vol. 403, (2000) p. 512.
[5]
G. A. Fiete,
E. J. Heller, http://lanl.arxiv.org/cond-mat/021167 (2003).
[6]
J. Marciak-Kozłowska, M. Kozłowski,
Quantum conductance and diffusion of nanostructures, Lasers in Engineering
6, (1997), p. 1.
[7]
M. Kozłowski, J. Marciak-Kozłowska,
Quantum mechanics for subnanotechnology, NanoWorkshop 2001, CELDIS, Warsaw,
September 2001.
[8]
J. Marciak-Kozłowska, M. Kozłowski,
Modified Schrödinger Equation for attosecond laser pulse interaction with
matter, Lasers in Engineering 12,
(2002), p. 53.
[9]
J. Marciak-Kozłowska, M. Kozłowski,
Schrödinger euqation for nanoscience, http://lanl.arxiv.org/cond.mat/030669
(2003).
Uzupełnienie A.
Równoważność jednocząstkowych stacjonarnych fal de Broglie’a i fal świetlnych
Niestacjonarna funkcja Greena opisuje efekt źródła
punktowego umieszczonego w punkcie czasoprzestrzeni ![]() obserwowany w punkcie
czasoprzestrzeni
obserwowany w punkcie
czasoprzestrzeni ![]() . W przypadku światła (fali elektromagnetycznej)
jednocząstkowa funkcja Greena ma postać [A.1]
. W przypadku światła (fali elektromagnetycznej)
jednocząstkowa funkcja Greena ma postać [A.1]
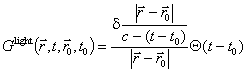 . (A.1)
. (A.1)
Dla cząstki kwantowej
o masie m funkcję Greena – falę de Broglie’a (dla nierelatywistycznego
równania Schrödingera) zapisujemy jako
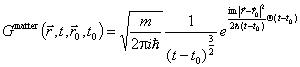 . (A.2)
. (A.2)
We wzorach (A.1) i
(A.2) ![]() oznacza funkcję delta
Diraca i
oznacza funkcję delta
Diraca i ![]() funkcję Heaviside’a.
funkcję Heaviside’a.
Rozważmy z kolei
stacjonarne jednocząstkowe funkcje Greena. W tym celu rozpatrujemy źródło,
które emituje w chwili ![]() elementarną
niestacjonarną falę harmoniczną o częstości
elementarną
niestacjonarną falę harmoniczną o częstości ![]() ,
, ![]() . Detektor umieszczony w punkcie
. Detektor umieszczony w punkcie ![]() , w chwili t zmierzy superpozycję wszystkich fal
wysłanych w chwili
, w chwili t zmierzy superpozycję wszystkich fal
wysłanych w chwili ![]() ze źródła
ze źródła ![]() :
:
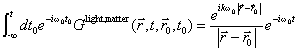 , (A.3)
, (A.3)
gdzie dyspersja fal
jest opisana za pomocą wzoru
![]() (A.4)
(A.4)
dla światła, oraz
![]() (A.5)
(A.5)
dla fali de Broglie’a
cząstki o masie m. Identyczna postać stacjonarnej jednocząstkowej
funkcji Greena dla fal de Broglie’a i fal świetlnych implikuje pełną
równoważność stacjonarnej optyki fal de Broglie’a i fal elektromagnetycznych.
Literatura
[A1] C. Brukner and A.
Zeilinger, Phys. Rev. Lett., 79 (1997) p. 2599.
Uzupełnienie B
Porównanie własności fal de Broglie’a – Bohma i fal elektromagnetycznych
|
|
Fale de Broglie'a (Elektrony) |
Fale elektromagnetyczne |
|
1. |
Istnieje skalarna zespolona amplituda |
Istnieje rzeczywista amplituda – funkcja wektorowa, |
|
2. |
Funkcja |
Natężenie fali wyznacza prawdopodobieństwo absorpcji kwantu
energii w trakcie oddziaływania promieniowania z materią. W przybliżeniu
klasycznym, gdy mamy do czynienia z wielką liczbą kwantów, prawdopodobieństwo
jest prawie równe jedności. Otrzymujemy wówczas klasyczny obraz oddziaływania
fali elektromagnetycznej z materią. |
|
3. |
Prawdopodobieństwo znalezienia elektronu w położeniu x,
x+dx określa wzór |
Ściśle biorąc nie istnieje funkcja określająca
prawdopodobieństwo znalezienia kwantu fali elektromagnetycznej w wybranym
punkcie. Jeżeli wybierzemy obszar duży w porównaniu z długością fali to: |
|
4. |
Prawdopodobieństwo znalezienia elektronu z pędem |
Dla jednego kwantu prawdopodobieństwo otrzymania pędu z
przedziału |
|
5. |
|
Tylko w próżni ponieważ kwanty promieniowania mogą być
emitowane lub absorbowane przez ruchome ładunki elektryczne. |
|
6. |
Istnieje prąd prawdopodobieństwa |
Nie ma odpowiednika |
Uzupełnienie C
Siły, moc, impedancja w ruchu harmonicznym (struna)
Fale biegnące mogą być
generowane w skończonych układach za pomocą drgań wymuszonych na brzegach
układu. Rozważmy ruch rozciągniętej struny obciążonej napięciem T,
mającej gęstość liniową ![]() . Niech warunki brzegowe określają wzory
. Niech warunki brzegowe określają wzory
![]() (C.1)
(C.1)
gdzie l oznacza
długość struny. Wektor falowy wybieramy w postaci
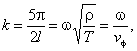 (C.2)
(C.2)
![]() jest prędkością fazową
fali
jest prędkością fazową
fali
![]() (C.3)
(C.3)
Warunki brzegowe
wywołują ruch struny w kierunku prostopadłym do struny. Składowa prostopadła
siły pobudzającej działająca na strunę w punkcie ![]() ma postać
ma postać
![]() (C.4)
(C.4)
Na końcu struny ![]() składowa siły jest
określona za pomocą wzoru
składowa siły jest
określona za pomocą wzoru
![]() (C.5)
(C.5)
W drganiach
wymuszonych struny, końce struny poruszają się w kierunku ![]() do x. Stąd moc
wymuszającą ruch opisuje wzór
do x. Stąd moc
wymuszającą ruch opisuje wzór
![]() (C.6)
(C.6)
Dla fali biegnącej moc
absorbowana i prędkość są proporcjonalne
![]() (C.7)
(C.7)
A zatem
![]() (C.8)
(C.8)
gdzie stała Z
![]() (C.10)
(C.10)
nosi nazwę impedancji
struny. Impedancja określa moc niezbędną do generacji fali biegnącej. Moc
niezbędna w punkcie ![]() równa się
równa się
![]() (C.11)
(C.11)
Średnia moc równa się
![]() (C.12)
(C.12)
W ogólnym przypadku
fala biegnąca jest opisywana przez wzór
![]() (C.13)
(C.13)
W tym przypadku
impedancja jest zdefiniowana następująco:
![]() (C.14)
(C.14)
Stąd
![]() (C.15)
(C.15)
Zespoloną impedancję
określa wzór
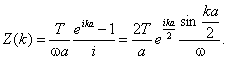 (C.16)
(C.16)
Średnia moc niezbędna
do generacji fali (C.13) jest określona za pomocą wzoru
![]()