Deadline 2017.02.05 24:00 to mail marian.dovgialo@fuw.edu.pl
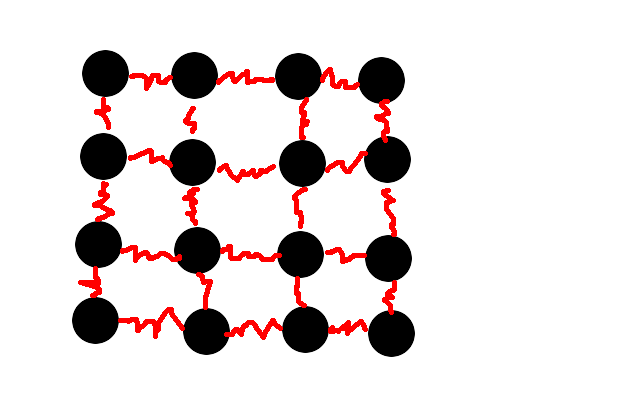
For this project you have to write a program, which simulates a network sized 100 by 100 of masses connected by springs. Springs have natural length of 1 cm and some coefficient k.

Program should ask user for a index of one mass (position x, y on the network) and displacement of that mass from resting position (x, y). After that your program should simulate 10 seconds of movement of such network with timestep 0.01s. Assume, that masses on edges of the network are not moving, and all starting velocities equal 0. Every simulation step should be visualized and written to image file. All image files should be named by the number of step they visualize. You should visualise only movement of masses, you don't have to draw springs.
Onto every mass there is a force applied which is a superposition of forces of all 4 springs. Just in case - force of the spring: F = k Δl,
where Δl - displacement of the string
Movement of the masses you can split into 2 components x i y and they can be written into these pseudo recursive equations:
x = x + vx * dt
y = y + vy * dt
vx = vy + ax*dt
vy = vy + ay*dt
ax = Fx/m
ay = Fx/m
where on the left are new positions/velocities, dt - simulation step, Fx Fy - force applied to the mass.
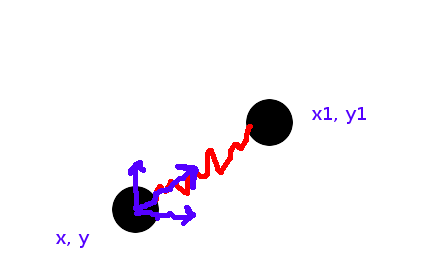
Using position of the masses you can calculate force which spring applies to mass:
Fx = k (((x1-x)2 + (y1-y)2)0.5-l0) * (x1-x)/((x1-x)2 + (y1-y)2)0.5
Fy = k (((x1-x)2 + (y1-y)2)0.5-l0) * (y1-y)/((x1-x)2 + (y1-y)2)0.5
where l0 - free length of spring, x y - position of the mass for which we calculate force, x1, y1 -