With activated notation
PolVec[P, pol], with
P being LVector and
pol interpretable as possible polarization, is denoted by
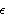 pol(P)
pol(P) :
When first argument of
PolVec is not LVector or second is not interpretable as possible polarization notation is not changed:
With activated notation
PolVec[P, pol, q], with
P being LVector,
pol interpretable as possible polarization and
q being massless Spinor, is denoted by
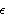 pol(P, q)
pol(P, q):
When first argument of
PolVec is not LVector, second is not interpretable as possible polarization or third is not massless Spinor notation is not changed:
To keep symbolic second argument of
PolVec but still use special notation, a symbol can be set to be interpreted as possible polarization using
DeclarePossiblePol:
PolVec[P, pol], with
P being LVector and
pol interpretable as possible polarization, is interpreted as LVector:
If first argument of
PolVec is not LVector or second is not interpretable as possible polarization, then
PolVec is not interpreted as LVector:
PolVec[P, pol, q], with
P being LVector,
pol interpretable as possible polarization and
q being massless Spinor, is interpreted as LVector:
If first argument of
PolVec is not LVector, second is not interpretable as possible polarization or third is not massless Spinor, then
PolVec is not interpreted as LVector:
To keep symbolic second argument of
PolVec but still make it interpretable as LVector,a symbol can be set to be interpreted as possible polarization using
DeclarePossiblePol:
PolVec[P, ±1], with
P being LVector, is interpreted as massless Spinor:
If first argument of
PolVec is not LVector or second is not interpretable as
±1, then
PolVec is not interpreted as massless Spinor:
PolVec[P, ±1, q], with
P being LVector and
q being massless Spinor, is interpreted as massless Spinor:
If first argument of
PolVec is not LVector, second is not interpretable as
±1 or third is not massless Spinor, then
PolVec is not interpreted as massless Spinor:
To keep symbolic second argument of
PolVec but still make it interpretable as massless Spinor, a symbol can be set to be interpreted as
+1 or
-1 using
DeclarePlusMinusOne: