


Next: Conclusion
Up: wfj08w
Previous: Introduction
Figure 1:
Stability of the calculated SHF+BCS energy curve for
 Pu as a function of the harmonic-oscillator basis size, see text.
Pu as a function of the harmonic-oscillator basis size, see text.
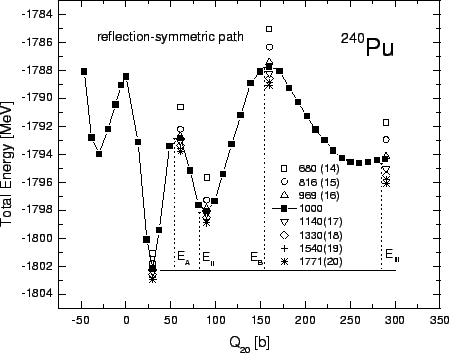 |
First, we have studied the stability of our results with respect
to the number of the deformed HO states
(
 ) used in this basis. Figure 1 shows the calculated
self-consistent potential energy curve of
) used in this basis. Figure 1 shows the calculated
self-consistent potential energy curve of  Pu as a
function of the axial quadrupole constraint
Pu as a
function of the axial quadrupole constraint
 . The solid line corresponds to
. The solid line corresponds to
 =1000 deformed HO states included in
the basis.
At each value of
=1000 deformed HO states included in
the basis.
At each value of  , the HO basis deformation is determined
as that corresponding to
, the HO basis deformation is determined
as that corresponding to  through the standard first-order
expression[11]. Therefore, the set of HO states
included in the basis changes with the changing nuclear shape.
The results with different values of
through the standard first-order
expression[11]. Therefore, the set of HO states
included in the basis changes with the changing nuclear shape.
The results with different values of
 =680
(14 spherical oscillator shells included at
=680
(14 spherical oscillator shells included at  =0), 816 (15), 969 (16), 1140 (17),
1330 (18), 1540 (19), and 1771 (20) are also shown at the extreme
points (minima and maxima) of the potential energy curve.
It is seen that the rate of convergence weakly depends on the quadrupole
deformation, and for larger elongations is slightly slower than at sphericity.
As shown in Fig. 1, reliable calculations can be carried
out with
=0), 816 (15), 969 (16), 1140 (17),
1330 (18), 1540 (19), and 1771 (20) are also shown at the extreme
points (minima and maxima) of the potential energy curve.
It is seen that the rate of convergence weakly depends on the quadrupole
deformation, and for larger elongations is slightly slower than at sphericity.
As shown in Fig. 1, reliable calculations can be carried
out with
 1140 (17), and the errors related to
the finite basis sizes that impact energies of
the first
1140 (17), and the errors related to
the finite basis sizes that impact energies of
the first  and second
and second  barrier are less than 1
MeV.
barrier are less than 1
MeV.
Having determined the basis size, we performed the set of
calculations for the series of even-even Fermium isotopes which
are experimentally known to exhibit rapid variations of the
spontaneous fission half-lives.
Two fission paths corresponding to bimodal fission have been
investigated. The usual reflection-asymmetric path corresponds to two
fission fragments with different masses. The reflection-symmetric path
can be associated with division into symmetric, nearly spherical
fragments with high kinetic energies.
In our calculations, the quadrupole and octupole mass
moments were used as constraints.
The non-zero
octupole mass moment  indicates the breaking of intrinsic
parity, while the presence of the quadrupole moment
indicates the breaking of intrinsic
parity, while the presence of the quadrupole moment  signals the appearance of triaxial distortions.
signals the appearance of triaxial distortions.
Figure:
Total
binding energy
 and the mass
octupole moments
and the mass
octupole moments  calculated along the
lowest static
fission paths for the even-even Fermium isotopes with
calculated along the
lowest static
fission paths for the even-even Fermium isotopes with
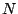 =142-152. The differences between the open and solid
symbols in the region of the first barrier represent the energy
gain due to triaxiality.
=142-152. The differences between the open and solid
symbols in the region of the first barrier represent the energy
gain due to triaxiality.
 =1140 was used.
=1140 was used.
 |
Figure 3:
Similar as in
Fig. 2 except for the even-even Fermium isotopes with  =154-164.
=154-164.
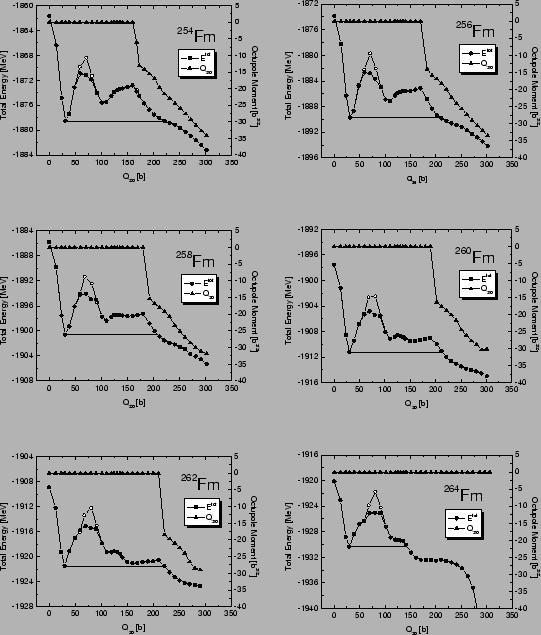 |
Deformation energy curves
(
 ) and the mass octupole moments (
) and the mass octupole moments ( ) calculated
along static fission paths for the even-even Fermium isotopes
with the neutron numbers
) calculated
along static fission paths for the even-even Fermium isotopes
with the neutron numbers  =142-164 are plotted in Figs. 2 and 3
as functions
of the mass quadrupole moment
=142-164 are plotted in Figs. 2 and 3
as functions
of the mass quadrupole moment  .
All calculated static barriers have similar, two-humped shapes.
The sizes of the static fission barriers are correlated
with the experimentally known increase in the
spontaneous fission half-lives for the lighter Fermium isotopes with
.
All calculated static barriers have similar, two-humped shapes.
The sizes of the static fission barriers are correlated
with the experimentally known increase in the
spontaneous fission half-lives for the lighter Fermium isotopes with
 =142-152. The influence of triaxial asymmetry on the height of
the first fission barrier is shown as a difference between the open
and solid symbols. The effect of triaxiality
increases with neutron number and reaches about 3MeV for
=142-152. The influence of triaxial asymmetry on the height of
the first fission barrier is shown as a difference between the open
and solid symbols. The effect of triaxiality
increases with neutron number and reaches about 3MeV for 
 150.
For
150.
For  b, the fission paths of nuclei displayed
in Fig. 2 exhibit reflection-symmetric shapes (
b, the fission paths of nuclei displayed
in Fig. 2 exhibit reflection-symmetric shapes ( ), while the
reflection-asymmetric paths (
), while the
reflection-asymmetric paths ( ) takes over at larger
elongations with
) takes over at larger
elongations with  b.
For the heavier Fm isotopes displayed in Fig. 3, the transition
to the reflection-asymmetric path occurs at greater values
of
b.
For the heavier Fm isotopes displayed in Fig. 3, the transition
to the reflection-asymmetric path occurs at greater values
of  and the transition point increases with
and the transition point increases with 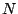 . In the
extreme case of
. In the
extreme case of  Fm (which is
expected to fission into two doubly magic
Fm (which is
expected to fission into two doubly magic  Sn nuclei),
the fission path becomes reflection-symmetric.
The disappearance of the reflection-asymmetric path at large
neutron numbers gives rise to the reduction, or even disappearance,
of the second
fission barrier. This reduction plays a crucial
role in the standard interpretation of the experimentally known
rapid decrease of the spontaneous fission half-lives in the heavy Fm
isotopes.
Sn nuclei),
the fission path becomes reflection-symmetric.
The disappearance of the reflection-asymmetric path at large
neutron numbers gives rise to the reduction, or even disappearance,
of the second
fission barrier. This reduction plays a crucial
role in the standard interpretation of the experimentally known
rapid decrease of the spontaneous fission half-lives in the heavy Fm
isotopes.
Figure:
Total
binding energy
 calculated along the static fission path
for the even-even Fermium isotopes
calculated along the static fission path
for the even-even Fermium isotopes  Fm. Open (closed) symbols
represent the reflection-asymmetric (symmetric) path. As compared
to Figs. 2 and 3,
the size of the oscillator basis is slightly reduced,
Fm. Open (closed) symbols
represent the reflection-asymmetric (symmetric) path. As compared
to Figs. 2 and 3,
the size of the oscillator basis is slightly reduced,
 =680.
=680.
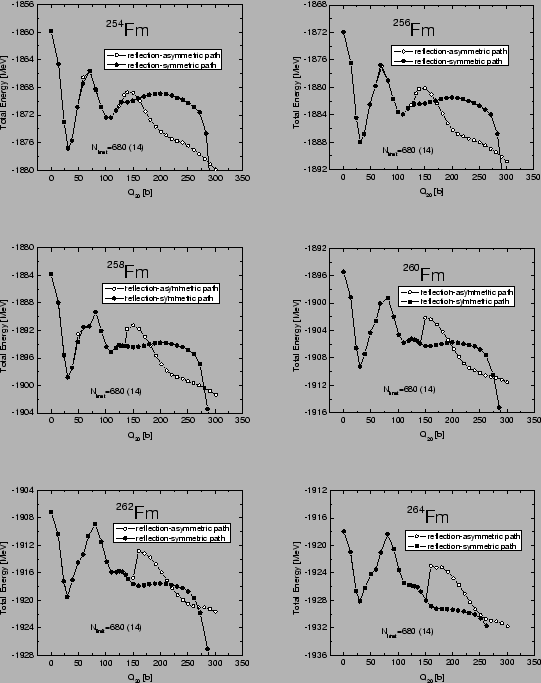 |
In order to better understand the competition between
reflection-symmetric
and reflection-asymmetric fission valleys, we show in Fig. 4
the total energy curves for
 Fm calculated with a smaller
basis
Fm calculated with a smaller
basis
 =680. For each nucleus
the two different fission paths are displayed: reflection-asymmetric
(open symbols) and reflection-symmetric (solid
symbols). It is seen that at large values of
=680. For each nucleus
the two different fission paths are displayed: reflection-asymmetric
(open symbols) and reflection-symmetric (solid
symbols). It is seen that at large values of  ,
the barriers along the reflection-asymmetric
paths are more narrow, whereas the distinctly higher second humps
appear.
,
the barriers along the reflection-asymmetric
paths are more narrow, whereas the distinctly higher second humps
appear.
Figure:
Total
binding energy
 and the mass
hexadecapole moment
and the mass
hexadecapole moment  as a function
of
as a function
of  for the even-even superheavy nuclei with
for the even-even superheavy nuclei with  . The
differences between the open and solid symbols represent the effect
of triaxiality on the first barrier.
. The
differences between the open and solid symbols represent the effect
of triaxiality on the first barrier.
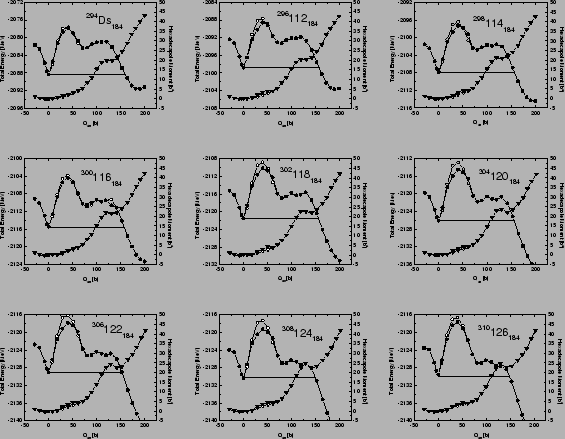 |
Figure 5 shows the deformation energy curves and the mass
hexadecapole moments calculated along the static fission paths of the
superheavy even-even nuclei with 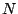 =184 (which is the neutron
magic gap in this region[12]). These results
markedly differ from those obtained for the Fm isotopes. As
expected[12], all
=184 (which is the neutron
magic gap in this region[12]). These results
markedly differ from those obtained for the Fm isotopes. As
expected[12], all 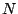 =184 isotones have spherical ground states.
The corresponding static two-humped fission barriers are narrow
and reflection-symmetric.
The triaxial deformation lowers the first barrier, with
the maximum reduction (2 MeV) predicted for
=184 isotones have spherical ground states.
The corresponding static two-humped fission barriers are narrow
and reflection-symmetric.
The triaxial deformation lowers the first barrier, with
the maximum reduction (2 MeV) predicted for  124.
As illustrated in Fig. 5, with increasing
124.
As illustrated in Fig. 5, with increasing  , the height of
the first barrier increases
while the second barrier gets reduced. The increase in the hexadecapole moment along the fission
path reflects the development of the neck.
, the height of
the first barrier increases
while the second barrier gets reduced. The increase in the hexadecapole moment along the fission
path reflects the development of the neck.



Next: Conclusion
Up: wfj08w
Previous: Introduction
Jacek Dobaczewski
2005-01-23


![]() indicates the breaking of intrinsic
parity, while the presence of the quadrupole moment
indicates the breaking of intrinsic
parity, while the presence of the quadrupole moment ![]() signals the appearance of triaxial distortions.
signals the appearance of triaxial distortions.


