


Next: Two Fermi Level Approach
Up: The Quasiparticle Formalism
Previous: States with even and
Signature symmetry
In this section we apply methods of occupying quasiparticle states,
outlined in Sec. 2.1, to a physical situation where the
system has a conserved signature symmetry, which can be used within
the cranking approximation
[21,17,18]. The signature operation [22]
is a rotation by  around one direction in space, which is
conventionally called the
around one direction in space, which is
conventionally called the  -axis:
-axis:
 |
(13) |
where  denotes the total angular-momentum operator along the
denotes the total angular-momentum operator along the  axis.
The signature operator is manifestly unitary,
axis.
The signature operator is manifestly unitary,
 .
Since a rotation by
.
Since a rotation by  reverses the phase of fermion wave functions,
the square of the signature operator gives the particle-number parity,
reverses the phase of fermion wave functions,
the square of the signature operator gives the particle-number parity,
 .
Therefore,
.
Therefore,  is hermitian and antihermitian in even and odd
spaces, respectively. In particular, in the single-particle space,
the signature is a unitary antihermitian operator.
is hermitian and antihermitian in even and odd
spaces, respectively. In particular, in the single-particle space,
the signature is a unitary antihermitian operator.
Since the signature  and time-reversal
and time-reversal  operators commute,
operators commute,
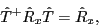 |
(14) |
signature is a time-even operator.
Therefore, for non-rotating systems (i.e., without time-odd fields),
signature is equivalent to the time-reversal symmetry  , but
it is more convenient to use, because
, but
it is more convenient to use, because  is a linear and not
an antilinear operator [23].
For states with nonzero angular momentum,
where
is a linear and not
an antilinear operator [23].
For states with nonzero angular momentum,
where  is internally broken,
is internally broken,  is often
still preserved [23,24,25]. The single-particle (and one-quasiparticle)
states may then be classified according to
the signature exponent quantum number
is often
still preserved [23,24,25]. The single-particle (and one-quasiparticle)
states may then be classified according to
the signature exponent quantum number  [26]:
[26]:
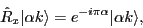 |
(15) |
where  takes the values of
takes the values of  .
For conserved signature,
the HFB mean fields
.
For conserved signature,
the HFB mean fields  and
and  commute and anticommute with
commute and anticommute with
 , respectively, and the HFB equations (7) can be written in a
good signature basis:
, respectively, and the HFB equations (7) can be written in a
good signature basis:
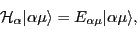 |
(16) |
where the HFB Hamiltonian matrix (6) in one signature reads
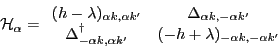 |
(17) |
and the two-component quasiparticle wave function is
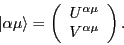 |
(18) |
A quasiparticle state with good signature is a linear
combination of states in time-reversed orbits [23]:
where  is the eigenvalue of the
is the eigenvalue of the  component of
the single-particle angular momentum,
component of
the single-particle angular momentum,  , and
we have adopted the phase convention according
to which
, and
we have adopted the phase convention according
to which
 [27,28], where
[27,28], where  is the parity quantum number. If the
Kramers degeneracy is present,
the description in terms of Kramers doublets and signature doublets
is equivalent. It is for polarized systems having time-odd mean fields
that the use of the signature symmetry is superior.
is the parity quantum number. If the
Kramers degeneracy is present,
the description in terms of Kramers doublets and signature doublets
is equivalent. It is for polarized systems having time-odd mean fields
that the use of the signature symmetry is superior.
The HFB equation (18) has the
(quasiparticle-quasihole) symmetry (7):
for each state
 of a given signature,
there exists a conjugate state of opposite signature
of a given signature,
there exists a conjugate state of opposite signature
 , opposite energy:
, opposite energy:
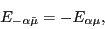 |
(21) |
and the quasiparticle wave function given by
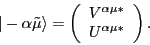 |
(22) |
By this symmetry, one needs to solve the HFB equation (18)
only for one signature, obtaining positive and negative quasiparticle
energies
 . Therefore, the entire set of negative quasiparticle
energies is composed of two groups: (i) the negative ones
. Therefore, the entire set of negative quasiparticle
energies is composed of two groups: (i) the negative ones
 obtained directly from the HFB equation solved for signature
obtained directly from the HFB equation solved for signature  , and
(ii) the inverted positive ones (23), which correspond to states
of signature
, and
(ii) the inverted positive ones (23), which correspond to states
of signature  .
.
The zero-quasiparticle HFB reference state (10), representing
the lowest configuration for a system with even number of fermions,
corresponds to a filled sea of Bogoliubov quasiparticles with
negative energies (Fig. 1(a)). In a one-quasiparticle
state, representing a state in an odd nucleus, a positive-energy
state is occupied and its conjugated partner is empty (Fig. 1(b)).
Figure 1:
(Color online)
Quasiparticle content of three configurations:
(a) vacuum; (b) the lowest one-quasi-particle state with  =1/2,
accessible via 2FLA; (c) the lowest
two-quasi-particle state with
=1/2,
accessible via 2FLA; (c) the lowest
two-quasi-particle state with  =0, not
accessible via 2FLA.
=0, not
accessible via 2FLA.
|
|
The exchange of the eigenvectors  and
and
 ,
that have opposite signatures,
corresponds to the exchange of columns in the
,
that have opposite signatures,
corresponds to the exchange of columns in the  and
and  matrices
discussed in Sec. 2.1 and reverses the particle-number parity
matrices
discussed in Sec. 2.1 and reverses the particle-number parity
 .
The density matrix and a pairing tensor of a one-quasiparticle state
(12) can be obtained from Eqs. (11)
[29,30]:
.
The density matrix and a pairing tensor of a one-quasiparticle state
(12) can be obtained from Eqs. (11)
[29,30]:
 where
where  and
and  correspond to the reference state (10).
correspond to the reference state (10).



Next: Two Fermi Level Approach
Up: The Quasiparticle Formalism
Previous: States with even and
Jacek Dobaczewski
2009-04-13
![]() around one direction in space, which is
conventionally called the
around one direction in space, which is
conventionally called the ![]() -axis:
-axis:
![]() and time-reversal
and time-reversal ![]() operators commute,
operators commute,
![]() of a given signature,
there exists a conjugate state of opposite signature
of a given signature,
there exists a conjugate state of opposite signature
![]() , opposite energy:
, opposite energy:
![\includegraphics[trim=0cm 0cm 0cm 0cm,width=0.45\textwidth,clip]{fig1.eps}](img107.png)
![]() and
and
![]() ,
that have opposite signatures,
corresponds to the exchange of columns in the
,
that have opposite signatures,
corresponds to the exchange of columns in the ![]() and
and ![]() matrices
discussed in Sec. 2.1 and reverses the particle-number parity
matrices
discussed in Sec. 2.1 and reverses the particle-number parity
![]() .
The density matrix and a pairing tensor of a one-quasiparticle state
(12) can be obtained from Eqs. (11)
[29,30]:
.
The density matrix and a pairing tensor of a one-quasiparticle state
(12) can be obtained from Eqs. (11)
[29,30]:
![]() where
where ![]() and
and ![]() correspond to the reference state (10).
correspond to the reference state (10).