


Next: About this document ...
Up: Quadrupole deformations of neutron-drip-line
Previous: Bibliography
Figure 1:
Total energies E, and proton and neutron rms radii, rp and
rn, obtained in the HFB+SLy4 calculations for 28O by using the HO
and THO bases, as functions of the number of HO shells
 .
The exact results refer to those obtained from spherical coordinate-space
calculations.
.
The exact results refer to those obtained from spherical coordinate-space
calculations.
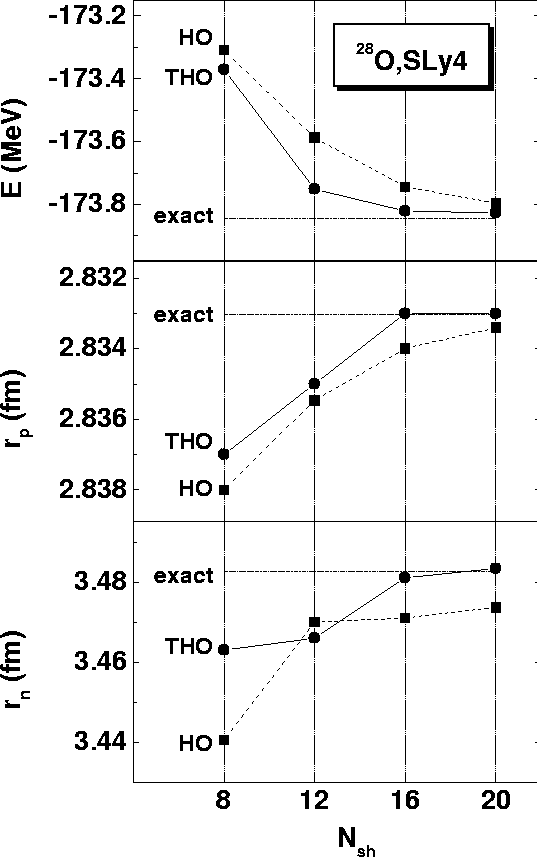 |
Figure 2:
Neutron densities obtained in the HFB+SLy4 calculations for
28O by using the HO (dashed line) and THO (solid line) bases. Neutron
and proton densities denoted as ``exact'' (dots) have been obtained from
spherical coordinate-space calculations in a box of
 =20fm.
=20fm.
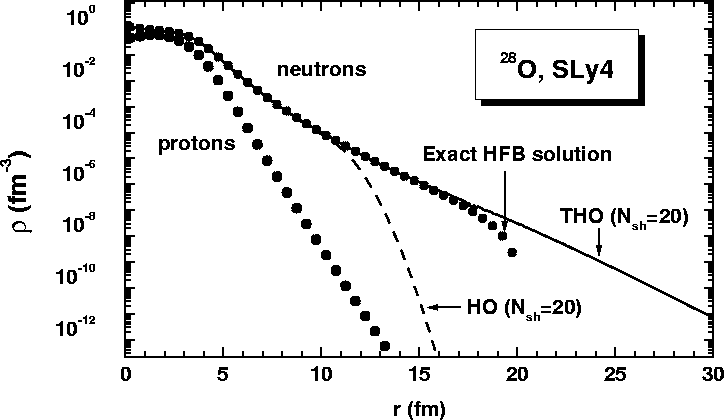 |
Figure 3:
Total energies E, proton and neutron rms radii, rp and rn, and deformations  obtained in the HFB+SLy4 calculations for
40Mg by using the HO and THO bases, as functions of the number of HO shells
obtained in the HFB+SLy4 calculations for
40Mg by using the HO and THO bases, as functions of the number of HO shells
 .
The horizontal lines denote the THO results obtained at
.
The horizontal lines denote the THO results obtained at
 =20.
=20.
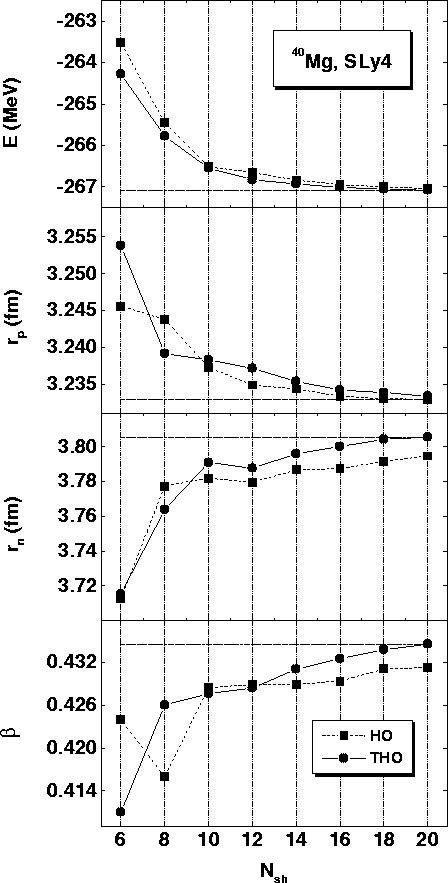 |
Figure 4:
Neutron densities obtained in the HFB+SLy4 calculations for the
deformed ground state of 44Mg by using the HO (circles) and THO
(squares) bases. Each point corresponds to one Gauss-integration node in the
z- plane, and the results are plotted as functions of the distance
from the origin, r=(z2+
plane, and the results are plotted as functions of the distance
from the origin, r=(z2+
 .
.
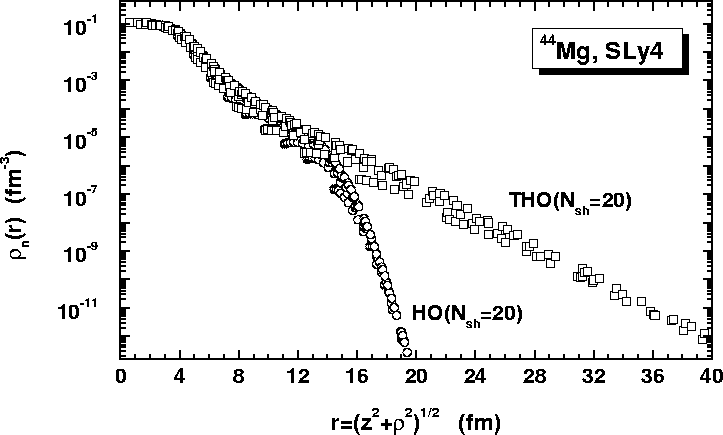 |
Figure 5:
Neutron Fermi energies  ,
energies per particle E/A,
deformations
,
energies per particle E/A,
deformations  ,
quadrupole moments Q, pairing gaps
,
quadrupole moments Q, pairing gaps
 ,
and pairing energies
,
and pairing energies
 calculated for the Mg
isotopes within the HFB+SLy4 method in the THO basis (
calculated for the Mg
isotopes within the HFB+SLy4 method in the THO basis (
 =20),
as functions of the mass number A. Apart from the upper panel, circles,
squares, and diamonds pertain to proton, neutron, and total results,
respectively. Closed symbols connected with lines denote values for the
absolute minima in the deformation-energy curve (axial shapes are assumed),
while open symbols pertain to secondary minima.
=20),
as functions of the mass number A. Apart from the upper panel, circles,
squares, and diamonds pertain to proton, neutron, and total results,
respectively. Closed symbols connected with lines denote values for the
absolute minima in the deformation-energy curve (axial shapes are assumed),
while open symbols pertain to secondary minima.
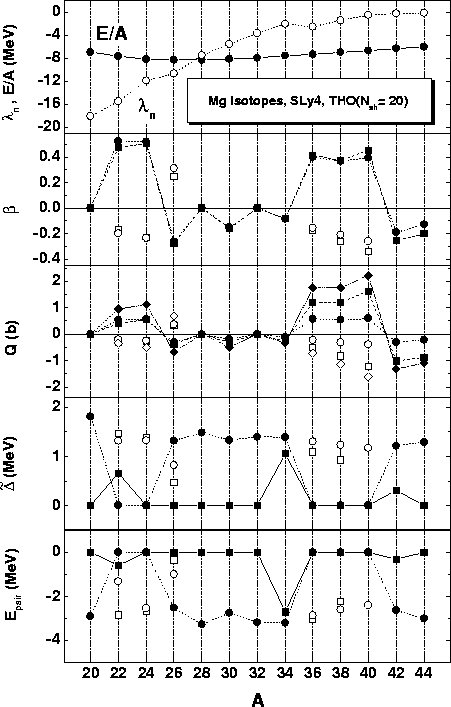 |
Figure 6:
Upper panel: two-neutron separation energies S2n (open
symbols) compared to
 (closed symbols), and lower panel: proton
and neutron rms radii. Calculations for the Mg isotopes were performed
within the HFB+SLy4 method in the THO basis for
(closed symbols), and lower panel: proton
and neutron rms radii. Calculations for the Mg isotopes were performed
within the HFB+SLy4 method in the THO basis for
 =20.
=20.
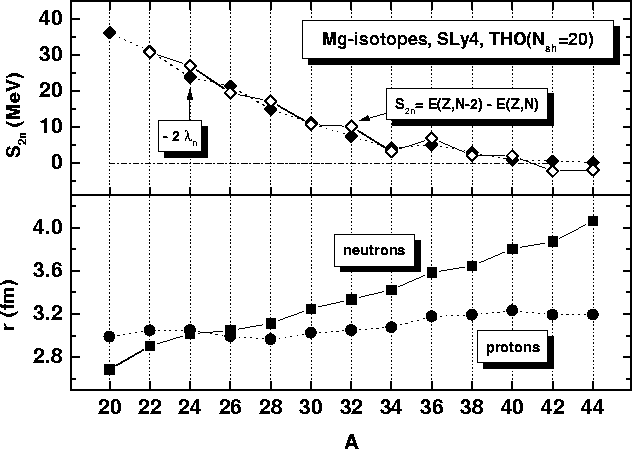 |
Figure 7:
Neutron Fermi energies  ,
energies per particle E/A,
pairing gaps
,
energies per particle E/A,
pairing gaps
 ,
pairing energies E, deformations
,
pairing energies E, deformations  ,
quadrupole moments Q, and rms radii r calculated for the
neutron-drip-line nuclei (indicated in the lower panel) within the HFB+SLy4
method in the THO basis, as functions of the mass number A. Circles,
squares, and diamonds pertain to proton, neutron, and total results,
respectively.
,
quadrupole moments Q, and rms radii r calculated for the
neutron-drip-line nuclei (indicated in the lower panel) within the HFB+SLy4
method in the THO basis, as functions of the mass number A. Circles,
squares, and diamonds pertain to proton, neutron, and total results,
respectively.
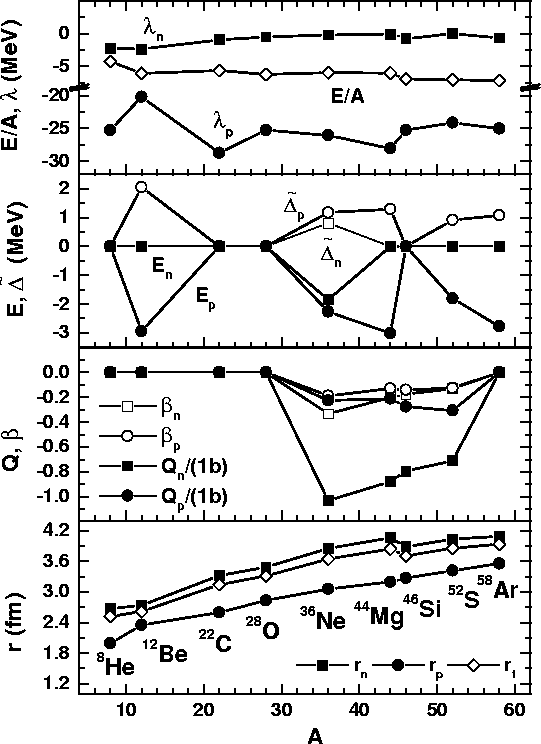 |



Next: About this document ...
Up: Quadrupole deformations of neutron-drip-line
Previous: Bibliography
Jacek Dobaczewski
1999-09-13







