Application to $^{156}$Gd

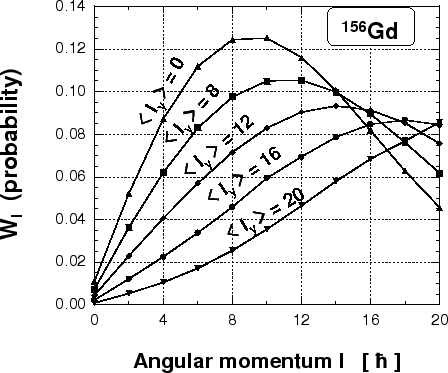
Figure 1: Probability distributions of even angular-momentum components $I$ in $^{156}$Gd.

We solve the cranked SHF equations for $^{156}$Gd by using the code HFODD for the SIII Skyrme-force parameters[16] and spherical harmonic-oscillator basis composed of $N_0$=10 shells. Then, we calculate the Hamiltonian and overlap kernels by using 50 Gauss-Chebyshev integration points in the $\alpha$ and $\gamma$ directions and 50 Gauss-Legendre points in the $\beta$ direction.[12] Figure 1 shows probability distributions $W_I$ of even angular-momentum components $I$ in the intrinsic cranked-SHF states $\vert\Phi_{I_y} \rangle$ constrained to $\langle \hat{I}_y \rangle = I_y$. The probability of finding the $I$ component can be calculated from:[1]

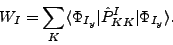$$W_I = \sum_{K} \langle \Phi_{I_y} \vert \hat{P}^I_{KK}\vert\Phi_{I_y} \rangle.$$ (10)

The curves correspond to cranking wave functions with averaged angular momenta $\langle I_y\rangle = 0, 8, 12, 16$, and $20\hbar$. One can see that for low angular momenta (e.g., for $I_y=0$) the maxima of the distributions do not lie near the same values of $I\simeq \langle I_y\rangle$. Similar results have been obtained by Islam et al.[7] and Baye et al.[8].

Figure 2: Probability distributions of projections $K$ in the even angular-momentum components $I$ projected from the state with $\langle I_y\rangle=10\hbar$ in $^{156}$Gd.

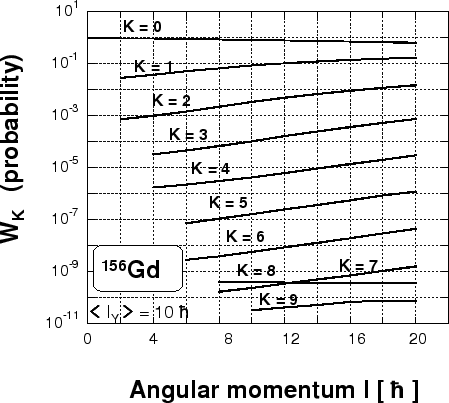In Fig. 2 we show similar probability distributions $W_K$ of the projections $K$,

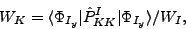$$W_K = \langle \Phi_{I_y} \vert \hat{P}^I_{KK}\vert\Phi_{I_y} \rangle/W_I,$$ (11)

projected from the state with $\langle I_y\rangle=10\hbar$ in $^{156}$Gd. One can see that the $K=0$ component dominates for all angular momenta, while the $K>0$ components increase with the increasing angular momentum. The $K=1$ component is the second in magnitude after $K=0$, which illustrates the build-up of the Coriolis coupling in a rotating intrinsic state. Note that only even values of $K$ can be projected from the non-rotating $\langle I_y\rangle=0$ state, while all $K\geq0$ appear in the cranked state.

In order to find energies of the AMP states, we solve Eq. (9) by diagonalizing first the norm matrix:

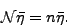$$\mathcal{N} \bar{\eta} = n \bar{\eta}.$$ (12)

The non-zero eigenvalues ($n_m\ne 0$) of $\mathcal{N}$ are used afterwards to built the so-called natural states

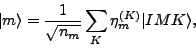$$\vert m\rangle = \frac{1}{\sqrt{n_m}} \sum_{K} \eta_m^{(K)} \vert IMK\rangle ,$$ (13)

that span the subspace called collective subspace. Final diagonalization of the HW equation (9) is performed within the collective subspace. In this subspace the problem reduces to the standard hermitian eigenvalue problem.

Figure 3: Dependence of energies of projected states on the number of the norm eigenstates kept in the collective subspace. Angular momenta $0\leq {I}\leq 20$ were projected from the state having the average projection of angular momentum $\langle\hat{I}_y\rangle=10\hbar$.

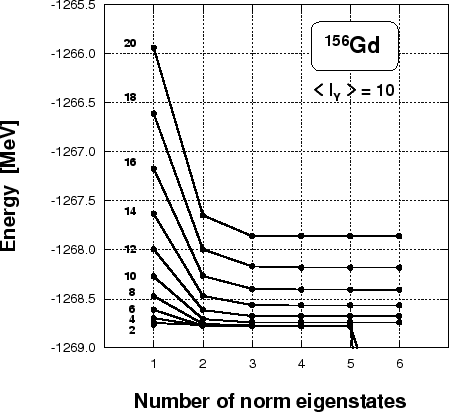In practical numerical applications we use the cut-off parameter $\zeta$ to construct the collective subspace, by keeping only the norm eigenstates (12) with $n_m\geq\zeta$. The test depicted in Fig. 3 shows the stability of projected solutions with respect to the number of the norm eigenstates kept in the collective subspace. The analysis was conducted for angular-momentum $0\leq {I}\leq 20$ states projected from the deformed solution $\vert\Phi_{I_y=10}\rangle$ obtained by solving the cranked SHF equations with the constraint $\langle \Phi_{I_y=10}\vert \hat{I}_y \vert\Phi_{I_y=10}\rangle = 10\hbar$. The test clearly shows that, starting from a certain point, the obtained solutions are stable (plateau condition). Only for very small values of $\zeta < 10^{-8}$ the method becomes numerically unstable.

Figure 4: Rotational bands in $^{156}$Gd nucleus: the four bands represent: (a) experimental data, (b) cranked SHF calculations, (c) band projected from the state $\vert\Phi_{I_y=0}\rangle$, and (d) band projected from the state $\vert\Phi_{I_y=I}\rangle$ into $I$, for $I=0,2,\ldots20$.

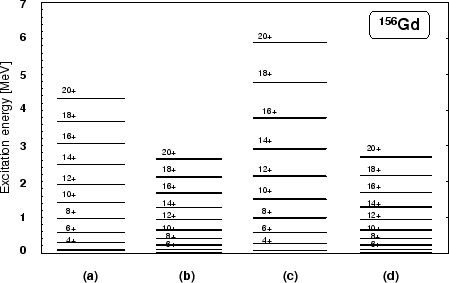Figure 4 shows rotational bands (b)-(d) calculated in $^{156}$Gd in comparison with the experimental data (a). Band (b) represents the average mean-field energies obtained from the cranked SHF calculations by constraining solutions to $\langle I_y\rangle=I$. In bands (c) and (d), we show energies obtained by the AMP from the $\langle I_y\rangle=0$ and $\langle I_y\rangle=I$, respectively. We see, that band (c) is much higher than bands (b) and (d), which indicates that the PAV from the $\langle I_y\rangle=0$ state is not an adequate method of describing nuclear rotation. Note that the mean-field energies (b) and the AMP energies (d) corresponding to $\langle I_y\rangle=I$ turn out to be very similar to one another. This shows that the AMP from the $\langle I_y\rangle=I$ states constitutes a correct symmetry restoration of the approximate VAP solutions realized by the cranking procedure. The remaining discrepancy with experimental data must be attributed to pairing correlations, which are not included in our SHF solutions.

When calculating the Hamiltonian kernels within the LEDF approach, one has to use transition density matrices between rotated states,

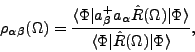$$\rho_{\alpha\beta}(\Omega)= \frac{\langle \Phi \vert a^+_\be... ...\rangle} {\langle \Phi\vert\hat{R}(\Omega)\vert\Phi \rangle},$$ (14)

which are singular whenever the rotated states are orthogonal. In particular, the transition multipole moments,

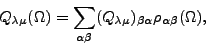$${Q}_{\lambda\mu}(\Omega)= \sum_{\alpha\beta}({Q}_{\lambda\mu})_{\beta\alpha}\rho_{\alpha\beta}(\Omega),$$ (15)

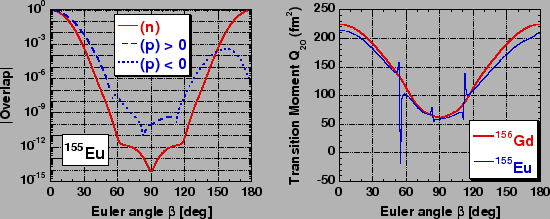
become singular for certain values of the Euler angles $\Omega$. This is illustrated in Fig.  5, which shows absolute values of the neutron and proton overlap kernels in $^{155}$Eu (left panel), and the transition quadrupole moments $Q_{20}(\Omega)$ in $^{155}$Eu and $^{156}$Gd (right panel). Calculations have been performed for axial shapes of nuclei, for which only the rotation about the Euler angle $\beta$ matters. The neutron overlap kernel corresponds to an even number of particles ($N=92$), and is always positive, although at $\beta=90^\circ$ it becomes as small as $10^{-14}$. On the other hand, the proton overlap kernel corresponds to an odd number of particles ($Z=63$), and it three times changes the sign in the interval of $0^\circ\leq\beta\leq180^\circ$. Consequently, the transition quadrupole moment of $^{156}$Gd is a regular function, while that of $^{155}$Eu has three poles.

Figure 5: Left panel: Dependence of the absolute value of the overlap between rotated states on the Euler angle $\beta$ in $^{155}$Eu. Solid line shows the neutron overlap that is always positive. Dashed and dotted lines show these segments of the proton overlap where it is positive and negative, respectively. Right panel: Transition quadrupole moments $Q_{20}$ versus $\beta$ in $^{156}$Gd (thick line) and $^{155}$Eu (thin line).

Of course, when calculating the matrix elements of multipole operators between the rotated states, the transition matrix elements (15) are multiplied by the overlap kernels and the poles disappear. However, such a compensation is absent for kernels corresponding to higher powers of densities, viz. for the density-dependent terms of the Skyrme interactions, or for the direct-Coulomb-energy terms, or for the exchange-Coulomb-energy terms in the Slater approximation. How to treat such singular kernels within the AMP methods is currently an open and unsolved problem, similarly as is the case for the particle-number-projection methods recently discussed in Ref.[17].