


Next: Conclusion
Up: Accuracy of solutions
Previous: The isoscalar 1 mode
The isovector 0 and isoscalar, isovector 2
and isoscalar, isovector 2 modes
modes
Figure 6
displays strength functions for the
0 and 2
and 2 channels in
channels in  Sn and
Sn and  Sn. (We discussed the
isoscalar
Sn. (We discussed the
isoscalar  mode above to illustrate the accuracy of our solutions, but
include it here as well for completeness.)
mode above to illustrate the accuracy of our solutions, but
include it here as well for completeness.)
Figure 6:
Isoscalar and isovector strength functions
for (a) the 0 channel of
channel of  Sn, (b) the 0
Sn, (b) the 0 channel of
channel of  Sn,
(c) the 2
Sn,
(c) the 2 channel of
channel of  Sn, and (d) the 2
Sn, and (d) the 2 channel of
channel of  Sn.
The cutoff
Sn.
The cutoff
 is 150 MeV and
is 150 MeV and
 is
is  .
.
![\includegraphics[width=14cm]{Sn120174}](img98.png) |
The calculations show the appearance of low-energy
 strength -- both isovector and isoscalar -- and low-energy isovector
2
strength -- both isovector and isoscalar -- and low-energy isovector
2 strength in
strength in  Sn, though in none of these instances is the
phenomenon quite as dramatic as in the isoscalar
Sn, though in none of these instances is the
phenomenon quite as dramatic as in the isoscalar  channel.
channel.
The EWSR for the isoscalar 2 transition operator,
transition operator,
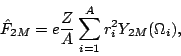 |
(8) |
can be written as [75]
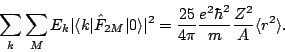 |
(9) |
The sum rule is obeyed as well in the 2 isoscalar channel as in the
isoscalar channel as in the  and
and  channels, the
only difference being that one needs to include quasiparticle states with
channels, the
only difference being that one needs to include quasiparticle states with  for
for
 Sn.
For
Sn.
For  Sn (
Sn ( Sn) from Fig. 6, the EWSR is 37222 (34971)
Sn) from Fig. 6, the EWSR is 37222 (34971)  MeVfm
MeVfm while the QRPA value is 37030 (35010)
while the QRPA value is 37030 (35010)
 MeVfm
MeVfm .
.
While on the topic of the sum rule, we
display
in Table 2 the  -dependence of
the EWSR
for several channels in
-dependence of
the EWSR
for several channels in  Sn, with
Sn, with
 fm.
By taking
fm.
By taking
 we appear to obtain essentially
the entire strength in all three
cases.
we appear to obtain essentially
the entire strength in all three
cases.
Table 2:
The  -dependence of isoscalar EWSR for
-dependence of isoscalar EWSR for  Sn.
Sn.  is
25 fm.
is
25 fm.
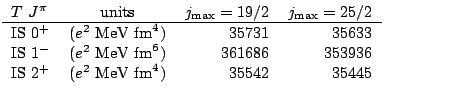 |



Next: Conclusion
Up: Accuracy of solutions
Previous: The isoscalar 1 mode
Jacek Dobaczewski
2004-07-29
![]() and 2
and 2![]() channels in
channels in ![]() Sn and
Sn and ![]() Sn. (We discussed the
isoscalar
Sn. (We discussed the
isoscalar ![]() mode above to illustrate the accuracy of our solutions, but
include it here as well for completeness.)
mode above to illustrate the accuracy of our solutions, but
include it here as well for completeness.)
![\includegraphics[width=14cm]{Sn120174}](img98.png)
![]() transition operator,
transition operator,
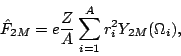
![]() -dependence of
the EWSR
for several channels in
-dependence of
the EWSR
for several channels in ![]() Sn, with
Sn, with
![]() fm.
By taking
fm.
By taking
![]() we appear to obtain essentially
the entire strength in all three
cases.
we appear to obtain essentially
the entire strength in all three
cases.