


Next: Angular-momentum projection near the
Up: Results
Previous: Results
Ground-state rotational band in  Ti
Ti
As a first example, consider the ground-state rotational band in
 Ti. According to the CHF model, the shape of this nucleus
undergoes a gradual change along the band. Starting from a well
elongated (
Ti. According to the CHF model, the shape of this nucleus
undergoes a gradual change along the band. Starting from a well
elongated (
 ) shape at low spins, the nucleus goes
through the alignment processes of the
) shape at low spins, the nucleus goes
through the alignment processes of the  protons and
neutrons, and eventually reaches a nearly spherical (
protons and
neutrons, and eventually reaches a nearly spherical (
 ) shape at the terminating spin of
) shape at the terminating spin of  , as shown in
Fig. 1a.
, as shown in
Fig. 1a.
Figure 1:
Results of the CHF and AMP calculations for the rotational
band in  Ti obtained for the SLy4 interaction. The upper panel
(a) shows the evolution of quadrupole and hexadecapole shape
parameters along the band as calculated using CHF approximation. The middle panel (b) shows the excitation
spectra calculated using the CHF approximation (left column) and AMP
method with kinematic and dynamic
Ti obtained for the SLy4 interaction. The upper panel
(a) shows the evolution of quadrupole and hexadecapole shape
parameters along the band as calculated using CHF approximation. The middle panel (b) shows the excitation
spectra calculated using the CHF approximation (left column) and AMP
method with kinematic and dynamic  -mixing (middle columns),
compared with the empirical data [25] (right column). The lower panel (c)
shows deviations
-mixing (middle columns),
compared with the empirical data [25] (right column). The lower panel (c)
shows deviations  of energy levels with spins
of energy levels with spins
 from the converged values corresponding the plateau
condition, as functions of the number
from the converged values corresponding the plateau
condition, as functions of the number
 of the norm
eigenvalues used when solving the HW equation.
of the norm
eigenvalues used when solving the HW equation.
![\includegraphics[width=\textwidth, clip]{prokra.fig1.eps}](img79.png) |
Figure:
Similar as in Fig. 1b, but shown in the absolute
energy scale. Results of the AMP from the
 ground state
(first column) are compared to those of the CHF (second column), AMP with
kinematic and dynamic
ground state
(first column) are compared to those of the CHF (second column), AMP with
kinematic and dynamic  -mixing (third and fourth columns), and CHFB calculations
(fifth column).
-mixing (third and fourth columns), and CHFB calculations
(fifth column).
![\includegraphics[width=\textwidth, clip]{prokra.fig2.eps}](img81.png) |
The calculated and experimental  Ti rotational bands are shown
in Fig. 1b. Results of the CHF calculations (left) are
compared to those of AMP (middle) and to experimental data (right). In order
to visualize the role of the
Ti rotational bands are shown
in Fig. 1b. Results of the CHF calculations (left) are
compared to those of AMP (middle) and to experimental data (right). In order
to visualize the role of the  -mixing, we have depicted results of
the AMP calculations separately for the kinematic and dynamic
-mixing, we have depicted results of
the AMP calculations separately for the kinematic and dynamic
 -mixing. For the dynamic
-mixing. For the dynamic  -mixing, the AMP excitation energies
were calculated from the plateau condition. The stability of results
with respect to the number of natural states
-mixing, the AMP excitation energies
were calculated from the plateau condition. The stability of results
with respect to the number of natural states
 is shown in Fig. 1c. It can be seen that
already at
is shown in Fig. 1c. It can be seen that
already at
 , a perfect stability is obtained, i.e.,
here, the difference between the kinematic and dynamic
, a perfect stability is obtained, i.e.,
here, the difference between the kinematic and dynamic  -mixing
is related to adding the
-mixing
is related to adding the  state to the collective subspace.
At higher values of
state to the collective subspace.
At higher values of
 , one observes small departures
from the converged values, which are due to accidental mixing
with spurious solutions (the largest such an effect is seen for
, one observes small departures
from the converged values, which are due to accidental mixing
with spurious solutions (the largest such an effect is seen for  at
at
 ). Nevertheless, physical converged solutions are
clearly seen well beyond the point where the spurious solutions become lower
in energy, as is well known for other generator-coordinate-method
calculations [26].
). Nevertheless, physical converged solutions are
clearly seen well beyond the point where the spurious solutions become lower
in energy, as is well known for other generator-coordinate-method
calculations [26].
Figure 1b clearly shows that within the 
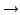
 scheme, the AMP effectively causes a decrease of the mean MoI within
the band. This effect is expected to be generic for rotational bands
of decreasing collectivity. Indeed, in such cases rotational
correction is large at low spins and decreases at higher spins. This
is illustrated in Fig. 2, where the calculated bands are
shown in the absolute energy scale. In the case of
scheme, the AMP effectively causes a decrease of the mean MoI within
the band. This effect is expected to be generic for rotational bands
of decreasing collectivity. Indeed, in such cases rotational
correction is large at low spins and decreases at higher spins. This
is illustrated in Fig. 2, where the calculated bands are
shown in the absolute energy scale. In the case of  Ti, a net
increase in the excitation energy of the terminating state, due to
the AMP, amounts to about 2MeV, but it is almost entirely related
to the lowering of the
Ti, a net
increase in the excitation energy of the terminating state, due to
the AMP, amounts to about 2MeV, but it is almost entirely related
to the lowering of the  state, while the terminating
state, while the terminating  state remains almost unaffected by the AMP.
state remains almost unaffected by the AMP.
In the same Figure, we also show for comparison the AMP spectrum
obtained by projecting from the
 ground
state. In this case, the overall MoI turns out to be much too small
and the excitation energy much too high as compared to the CHF or AMP
ground
state. In this case, the overall MoI turns out to be much too small
and the excitation energy much too high as compared to the CHF or AMP

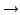
 results. This fact once again shows the
importance of the structural changes that occur in the system with
increasing angular momentum.
results. This fact once again shows the
importance of the structural changes that occur in the system with
increasing angular momentum.
Note that the
 state is axial, and thus
for all spins contains only the
state is axial, and thus
for all spins contains only the  component. Therefore, here, the
collective space contains only one state and there is no
component. Therefore, here, the
collective space contains only one state and there is no  -mixing
at all. Moreover, axial symmetry leads to a tremendous simplification
of the AMP method, whereby only one-dimensional integration over
the Euler
-mixing
at all. Moreover, axial symmetry leads to a tremendous simplification
of the AMP method, whereby only one-dimensional integration over
the Euler  angle is needed. Note also that the CHF states for
angle is needed. Note also that the CHF states for
 are never axial, because the Coriolis
coupling always induces some non-zero nonaxiality. Therefore, the
full three-dimensional integration over the Euler angles
are never axial, because the Coriolis
coupling always induces some non-zero nonaxiality. Therefore, the
full three-dimensional integration over the Euler angles
 is needed in our
is needed in our 
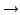
 scheme.
scheme.
In the right column of Fig. 2, we also show results of
the cranked Hartree-Fock-Bogolyubov calculations (CHFB) performed by
using a zero-range volume-type (density-independent) interaction in
the pairing channel. Its strengths of
 and
and
 MeVfm
MeVfm for neutrons and protons, respectively,
with the cutoff energy of
for neutrons and protons, respectively,
with the cutoff energy of
 MeV
[27], was adjusted so as to reproduce, on average, the
pairing gaps in this region of nuclei. For the
MeV
[27], was adjusted so as to reproduce, on average, the
pairing gaps in this region of nuclei. For the
 ground state of
ground state of  Ti, the calculated
gaps read
Ti, the calculated
gaps read
 and
and
 MeV.
MeV.
One can see that,
in comparison with the CHF results,
pairing correlations only affect states at low spins,  ,
and give about 1MeV of additional binding at
,
and give about 1MeV of additional binding at
 .
Pairing correlations vanish in the terminating state, and thus its
energy is the same within the CHF and CHFB methods. At present, the
code HFODD cannot perform the AMP of paired states, and we are yet unable
to evaluate combined effects of pairing and AMP from cranked states.
.
Pairing correlations vanish in the terminating state, and thus its
energy is the same within the CHF and CHFB methods. At present, the
code HFODD cannot perform the AMP of paired states, and we are yet unable
to evaluate combined effects of pairing and AMP from cranked states.
It is also interesting to observe that, in the case of  Ti, the
dynamic
Ti, the
dynamic  -mixing is effective essentially only for
-mixing is effective essentially only for  and 4,
see Fig. 1b,c. This result is rather surprising,
particularly in view of the fact that the only discontinuity in
spatial anisotropy of the CHF solutions can be seen around spins
and 4,
see Fig. 1b,c. This result is rather surprising,
particularly in view of the fact that the only discontinuity in
spatial anisotropy of the CHF solutions can be seen around spins
 . This behavior is also qualitatively different from
that found in
. This behavior is also qualitatively different from
that found in  Gd [12], where the dynamic
Gd [12], where the dynamic
 -mixing was effective up to the highest (
-mixing was effective up to the highest ( ) calculated
spins. Apparently, the magnitude of
) calculated
spins. Apparently, the magnitude of  -mixing cannot be inferred
solely from the shape but it also depends on individual (alignment)
degrees of freedom.
-mixing cannot be inferred
solely from the shape but it also depends on individual (alignment)
degrees of freedom.
Figure 3:
Probabilities  (12)
and
(12)
and  (13) of finding the given
(13) of finding the given  and
and  components,
respectively, in the intrinsic CHF states for different values of the
projection on the
components,
respectively, in the intrinsic CHF states for different values of the
projection on the  axis
axis
 . Solid lines are
drawn only to guide the eye. Note that due to the conserved
. Solid lines are
drawn only to guide the eye. Note that due to the conserved  -signature
symmetry, one has
-signature
symmetry, one has  =0 for odd values of
=0 for odd values of  and
and
 .
.
![\includegraphics[width=\textwidth, clip]{prokra.fig3.eps}](img100.png) |
In Fig. 3, we show probabilities  of finding the angular-momentum
components in the intrinsic CHF states, i.e.,
of finding the angular-momentum
components in the intrinsic CHF states, i.e.,
 |
(12) |
The inset also shows probabilities  of finding the given
of finding the given  components,
components,
 |
(13) |
in one of the intrinsic states,
 . At low
spins, the
. At low
spins, the  probability distributions follow the general pattern
of deformed collective states. This pattern suddenly disappears at
the termination point of
probability distributions follow the general pattern
of deformed collective states. This pattern suddenly disappears at
the termination point of
 , where the CHF
state becomes totally aligned, and therefore, it contains only the
single
, where the CHF
state becomes totally aligned, and therefore, it contains only the
single  component. The
component. The  probabilities do not follow the
standard pattern of collective rotation, where they correspond to the
Coriolis mixing only, cf. Fig. 2 in Ref. [12]. Here, the
aligning state causes the values of
probabilities do not follow the
standard pattern of collective rotation, where they correspond to the
Coriolis mixing only, cf. Fig. 2 in Ref. [12]. Here, the
aligning state causes the values of  to decrease with
to decrease with  and
induces the crossing of those corresponding to even and odd
and
induces the crossing of those corresponding to even and odd  values in function
of
values in function
of  . Note also, that the angular momentum aligns along the
. Note also, that the angular momentum aligns along the  axis, while the standard projections
axis, while the standard projections  are calculated with respect
to the
are calculated with respect
to the  axis. Therefore, we do not expect to see a single
axis. Therefore, we do not expect to see a single  component of the aligned
component of the aligned
 state.
state.
Figure:
Excitation spectra calculated using the AMP of CHF states constrained
to different values of
 , with kinematic
, with kinematic
 -mixing. Solid lines connect states of given projected angular
momenta
-mixing. Solid lines connect states of given projected angular
momenta  and are drawn only to guide the eye. Arrows indicate the
minimum energies in function of
and are drawn only to guide the eye. Arrows indicate the
minimum energies in function of
 . For
comparison, the right column shows the CHF spectrum.
. For
comparison, the right column shows the CHF spectrum.
![\includegraphics[width=\textwidth, clip]{prokra.fig4.eps}](img106.png) |
We conclude this section by analyzing excitation spectra calculated
using the AMP of CHF states constrained to different values of
 , as shown in Fig. 4. It turns out
that the AMP energies minimized with respect to
, as shown in Fig. 4. It turns out
that the AMP energies minimized with respect to
 , or equivalently with respect to the
angular frequency
, or equivalently with respect to the
angular frequency  , significantly differ from those obtained
within our
, significantly differ from those obtained
within our 
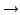
 scheme. Indeed, although the minimum
scheme. Indeed, although the minimum
 energy is obtained by projecting the
energy is obtained by projecting the
 CHF state, this is not the case for
CHF state, this is not the case for
 states. For example, the minimum
states. For example, the minimum  and 14 energies are
obtained by projecting the
and 14 energies are
obtained by projecting the
 and 10 CHF
states, respectively. The resulting excitation spectrum (in
Fig. 4 indicated by arrows) is quite irregular and can hardly
be associated with the physical result. The reason is the fact that
the minimization over
and 10 CHF
states, respectively. The resulting excitation spectrum (in
Fig. 4 indicated by arrows) is quite irregular and can hardly
be associated with the physical result. The reason is the fact that
the minimization over  does not constitute the full
variation-after-projection
minimization of energy, which should be performed in the complete
parameter space, including, e.g., the deformation parameters.
Moreover, the fact that the
does not constitute the full
variation-after-projection
minimization of energy, which should be performed in the complete
parameter space, including, e.g., the deformation parameters.
Moreover, the fact that the  state may gain energy by using
collective correlations on top of the fully aligned (terminating) state
points out a possible inadequacy of the EDF method
when it is used within the variation-after-projection procedure, and not within the
state may gain energy by using
collective correlations on top of the fully aligned (terminating) state
points out a possible inadequacy of the EDF method
when it is used within the variation-after-projection procedure, and not within the

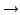
 projection-after-variation scheme.
projection-after-variation scheme.



Next: Angular-momentum projection near the
Up: Results
Previous: Results
Jacek Dobaczewski
2007-08-08
![]() Ti. According to the CHF model, the shape of this nucleus
undergoes a gradual change along the band. Starting from a well
elongated (
Ti. According to the CHF model, the shape of this nucleus
undergoes a gradual change along the band. Starting from a well
elongated (
![]() ) shape at low spins, the nucleus goes
through the alignment processes of the
) shape at low spins, the nucleus goes
through the alignment processes of the ![]() protons and
neutrons, and eventually reaches a nearly spherical (
protons and
neutrons, and eventually reaches a nearly spherical (
![]() ) shape at the terminating spin of
) shape at the terminating spin of ![]() , as shown in
Fig. 1a.
, as shown in
Fig. 1a.
![\includegraphics[width=\textwidth, clip]{prokra.fig1.eps}](img79.png)
![\includegraphics[width=\textwidth, clip]{prokra.fig2.eps}](img81.png)
![]()
![]()
![]() scheme, the AMP effectively causes a decrease of the mean MoI within
the band. This effect is expected to be generic for rotational bands
of decreasing collectivity. Indeed, in such cases rotational
correction is large at low spins and decreases at higher spins. This
is illustrated in Fig. 2, where the calculated bands are
shown in the absolute energy scale. In the case of
scheme, the AMP effectively causes a decrease of the mean MoI within
the band. This effect is expected to be generic for rotational bands
of decreasing collectivity. Indeed, in such cases rotational
correction is large at low spins and decreases at higher spins. This
is illustrated in Fig. 2, where the calculated bands are
shown in the absolute energy scale. In the case of ![]() Ti, a net
increase in the excitation energy of the terminating state, due to
the AMP, amounts to about 2MeV, but it is almost entirely related
to the lowering of the
Ti, a net
increase in the excitation energy of the terminating state, due to
the AMP, amounts to about 2MeV, but it is almost entirely related
to the lowering of the ![]() state, while the terminating
state, while the terminating ![]() state remains almost unaffected by the AMP.
state remains almost unaffected by the AMP.
![]() ground
state. In this case, the overall MoI turns out to be much too small
and the excitation energy much too high as compared to the CHF or AMP
ground
state. In this case, the overall MoI turns out to be much too small
and the excitation energy much too high as compared to the CHF or AMP
![]()
![]()
![]() results. This fact once again shows the
importance of the structural changes that occur in the system with
increasing angular momentum.
results. This fact once again shows the
importance of the structural changes that occur in the system with
increasing angular momentum.
![]() state is axial, and thus
for all spins contains only the
state is axial, and thus
for all spins contains only the ![]() component. Therefore, here, the
collective space contains only one state and there is no
component. Therefore, here, the
collective space contains only one state and there is no ![]() -mixing
at all. Moreover, axial symmetry leads to a tremendous simplification
of the AMP method, whereby only one-dimensional integration over
the Euler
-mixing
at all. Moreover, axial symmetry leads to a tremendous simplification
of the AMP method, whereby only one-dimensional integration over
the Euler ![]() angle is needed. Note also that the CHF states for
angle is needed. Note also that the CHF states for
![]() are never axial, because the Coriolis
coupling always induces some non-zero nonaxiality. Therefore, the
full three-dimensional integration over the Euler angles
are never axial, because the Coriolis
coupling always induces some non-zero nonaxiality. Therefore, the
full three-dimensional integration over the Euler angles
![]() is needed in our
is needed in our ![]()
![]()
![]() scheme.
scheme.
![]() and
and
![]() MeVfm
MeVfm![]() for neutrons and protons, respectively,
with the cutoff energy of
for neutrons and protons, respectively,
with the cutoff energy of
![]() MeV
[27], was adjusted so as to reproduce, on average, the
pairing gaps in this region of nuclei. For the
MeV
[27], was adjusted so as to reproduce, on average, the
pairing gaps in this region of nuclei. For the
![]() ground state of
ground state of ![]() Ti, the calculated
gaps read
Ti, the calculated
gaps read
![]() and
and
![]() MeV.
MeV.
![]() ,
and give about 1MeV of additional binding at
,
and give about 1MeV of additional binding at
![]() .
Pairing correlations vanish in the terminating state, and thus its
energy is the same within the CHF and CHFB methods. At present, the
code HFODD cannot perform the AMP of paired states, and we are yet unable
to evaluate combined effects of pairing and AMP from cranked states.
.
Pairing correlations vanish in the terminating state, and thus its
energy is the same within the CHF and CHFB methods. At present, the
code HFODD cannot perform the AMP of paired states, and we are yet unable
to evaluate combined effects of pairing and AMP from cranked states.
![]() Ti, the
dynamic
Ti, the
dynamic ![]() -mixing is effective essentially only for
-mixing is effective essentially only for ![]() and 4,
see Fig. 1b,c. This result is rather surprising,
particularly in view of the fact that the only discontinuity in
spatial anisotropy of the CHF solutions can be seen around spins
and 4,
see Fig. 1b,c. This result is rather surprising,
particularly in view of the fact that the only discontinuity in
spatial anisotropy of the CHF solutions can be seen around spins
![]() . This behavior is also qualitatively different from
that found in
. This behavior is also qualitatively different from
that found in ![]() Gd [12], where the dynamic
Gd [12], where the dynamic
![]() -mixing was effective up to the highest (
-mixing was effective up to the highest (![]() ) calculated
spins. Apparently, the magnitude of
) calculated
spins. Apparently, the magnitude of ![]() -mixing cannot be inferred
solely from the shape but it also depends on individual (alignment)
degrees of freedom.
-mixing cannot be inferred
solely from the shape but it also depends on individual (alignment)
degrees of freedom.
![\includegraphics[width=\textwidth, clip]{prokra.fig3.eps}](img100.png)
![\includegraphics[width=\textwidth, clip]{prokra.fig4.eps}](img106.png)