Conclusions

This study contains the systematic analysis of the particle-number-projected DFT approach. This approach, usually in the Skyrme-HFB or Gogny-HFB framework, is commonly used in systematic calculations of nuclear ground-state properties, low-energy excitations, and high-spin states. For heavy, complex nuclei, the nuclear DFT is the only viable microscopic tool based on the effective interaction (or functional). To advance the nuclear DFT further, to improve its theoretical foundations, and to make it a more reliable tool, it is important to fully understand the advantages and drawbacks of the method when applied to self-bound nuclear systems.

The main conclusions of this work can be summarized as follows:

1. The transition density matrices connecting states having different orientation in the gauge plane $z$ have poles on the imaginary axis ${\mbox{\rm\scriptsize {Im}}[z]}$. In the HFB formalism that is based on one Hamiltonian acting in all channels (Hamiltonian-based HFB), these poles are irrelevant as their impact is nullified by the cancellation between the Hamiltonian matrix elements originating from particle-hole and pairing channels. Such a cancellation is not present in the HFB applications in which some of the Hamiltonian matrix elements are neglected (or approximated), in the HFB method based on density-dependent interactions (usually acting in different channels), and in the DFT approach in which the Hamiltonian does not appear at all. In all those cases, the projection operator is not defined uniquely and the result depends on the analytic structure of the transition energy density; hence, the projected DFT energy depends on the integration contour. 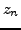The resulting PNP energy can be expressed in terms of individual residues corresponding to the poles $z_n$ associated with single-particle (canonical) proton and neutron orbits. In contrast, in the Hamiltonian-based HFB, the result depends only on the single pole at the origin ($z_0=0$).

2. Within the Hamiltonian-based HFB, there exist sum rules that relate the unprojected matrix elements with the matrix elements in the projected states. Similar sum rules can be derived within the DFT; they relate the unprojected DFT transition energy density with the projected DFT energies. The DFT sum rules offer the interpretation of the projected DFT energies as Fourier components (associated with irreducible representations of gauge group U(1)) of the DFT transition energy density. This can be naturally extended to other (higher) broken symmetry groups, such as SU(2) (associated with the broken angular momentum symmetry).

3. The discussion of the particle number restoration can be extended to other symmetry restoration problems. In particular, DFT transition densities associated with angular-momentum-projected states are expected to have complicated pole structure in the three dimensional space of Euler angles (see the example shown in Ref. [45]).

4. For the terms in the density functional that have polynomial density dependence, the appearance of poles inside the contour gives rise to sudden jumps of the projected energy whenever the contour's pole content changes. Otherwise, the results are stable. This is not true for the terms having fractional-power density dependence (e.g., density-dependent pieces of many Skyrme and Gogny interactions or the Coulomb exchange term taken in the Slater approximation). Here, the dependence on the contour radius shows a strong subthreshold behavior that can only be cured by considering appropriate integration contours which do not go across the cuts in the complex $z$-plane. Other prescriptions give rise to uncontrolled energy behavior resulting from the fact that the corresponding integration contours do not close.

5. As a practical measure that allows avoiding problems related to the fractional-power density dependence, we propose using the integration contours which pass near and above the poles. Although such a prescription requires using rather dense meshes of integration points, it minimizes the risks of crossing the cuts in the complex plane. In this way, the ambiguities related to the non-analyticity of the DFT transition energy are reduced to those corresponding to the choice of poles included within the integration contour.

6. Projected DFT yields questionable results if a pole appears very close to the integration contour. While such a situation seldom happens in the ground-state calculations (less than 2% cases are affected), it frequently occurs in calculations of projected energy surfaces, such as those in the generator coordinate method (GCM). The appearance of poles in the vicinity of the contour as a function of the collective coordinate (e.g., deformation) gives rise to uncontrolled irregularities and jumps in the results; in particular, it makes it impossible to define the PNP potential energy surfaces.

7. Pole pathologies appear in a particularly strong way in the fully self-consistent VAP calculations. In this approach, transition density poles are not uniquely defined; moreover, their positions can change during the iteration process leading to numerical instabilities.

8. The analytic structure of the transition energy density becomes exceedingly complicated in nuclei with protons and neutrons paired, thus requiring simultaneous proton and neutron PNP. Of particular importance in the context of GCM applications is the extension of the present analysis to non-diagonal matrix elements between the PNP states.

Some of the problems listed above, in particular those related to the configuration-mixing DFT method and applications of the generalized Wick's theorem to DFT, have been recently addressed in a series of papers [33,34]. In these studies, a practical cure has been proposed that is based on removing specific spurious components of the DFT functional that can be associated with self-interaction and self-pairing. When applied to truncated Hamiltonians, this practical prescription turns out to be very effective [46]. However, this kind of solution does not remove ambiguities related to using complicated (e.g., fractional-power) dependence of the energy density functionals on particle densities. Finding ultimate cures to the problems discussed in our study will undoubtedly result in establishing better theoretical constraints on the form of the DFT energy density functionals for nuclear self-bound systems.

This work was supported in part by the Polish Ministry of Science; by the Academy of Finland and University of Jyväskylä within the FIDIPRO programme; by the U.S. Department of Energy under Contract Nos. DE-FG02-96ER40963 (University of Tennessee), DE-AC05-00OR22725 with UT-Battelle, LLC (Oak Ridge National Laboratory), DE-FG05-87ER40361 (Joint Institute for Heavy Ion Research), and DE-FC02-07ER41457 (University of Washington); and by the National Nuclear Security Administration under the Stewardship Science Academic Alliances program through DOE Research Grant DE-FG03-03NA00083.