


Next: Proton-neutron symmetry
Up: Local Density Approximation for
Previous: The HFB equations
Conserved symmetries
Conserved and broken symmetries are one of the most important
elements of description of many-body systems. Within the mean-field
approach, the theorem about self-consistent symmetries [167]
tells us that mean-field states may or may not have all the
symmetries of the Hamiltonian, depending on interactions and the
system studied. Within the HFB approach, the symmetry is conserved
when the generalized density matrix
 and the generalized
Hamiltonian
and the generalized
Hamiltonian
 both commute with the symmetry operator
both commute with the symmetry operator
 , i.e., [
, i.e., [
 ,
,
 ]=0 and
[
]=0 and
[
 ,
,
 ]=0, or
]=0, or
where
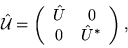 |
(210) |
and  is a unitary matrix of the single-particle symmetry operator.
For the ``breve'' representation used in the present study,
the symmetry operator is given) by [cf. Eq. (16)]
is a unitary matrix of the single-particle symmetry operator.
For the ``breve'' representation used in the present study,
the symmetry operator is given) by [cf. Eq. (16)]
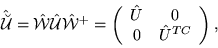 |
(211) |
and then
In the previous sections we have presented the most general set
of expressions pertaining to the situation when no symmetries were
a priori conserved. Below we discuss consequences of conserved
symmetries.
Subsections



Next: Proton-neutron symmetry
Up: Local Density Approximation for
Previous: The HFB equations
Jacek Dobaczewski
2004-01-03
![]() and the generalized
Hamiltonian
and the generalized
Hamiltonian
![]() both commute with the symmetry operator
both commute with the symmetry operator
![]() , i.e., [
, i.e., [
![]() ,
,
![]() ]=0 and
[
]=0 and
[
![]() ,
,
![]() ]=0, or
]=0, or