


Next: Densities
Up: General forms of the
Previous: Fields for terms containing
Rearrangement terms
For density-dependent terms, the total energy obtained from the
proton and neutron eigenvalues
 and kinetic
energies
and kinetic
energies 
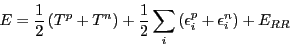 |
(64) |
includes the additional rearrangement term
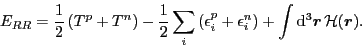 |
(65) |
For spherical symmetry the terms with density-dependent coupling constants in the Skyrme functional
only involve the  densities and for these a straightforward derivation gives
densities and for these a straightforward derivation gives
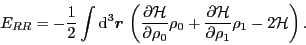 |
(66) |
Jacek Dobaczewski
2010-01-30
![]() and kinetic
energies
and kinetic
energies ![]()