


Next: The Hartree-Fock-Bogolyubov equations
Up: The Skyrme Hartree-Fock-Bogolyubov equations
Previous: The Hartree-Fock-Bogolyubov energy
Since the Bogolyubov transformation does not preserve the particle
number, we introduce two Lagrange multipliers  and
and
 to conserve the average neutron and proton number.
The HFB equations are then obtained by writing the stationary
condition
to conserve the average neutron and proton number.
The HFB equations are then obtained by writing the stationary
condition
![$ \delta \left[\mathcal{E}-\langle\lambda_N N +\lambda_Z Z\rangle\right]=0$](img97.png) .
The dependence of
.
The dependence of
 on the kinetic densities leads
the effective mass
on the kinetic densities leads
the effective mass
and to the abnormal effective mass
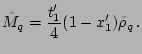 |
(24) |
The particle-hole (Hartree-Fock) fields is given by
In the case of protons,
varying the expressions (21)
and (22) leads to the following expression for the Coulomb
field
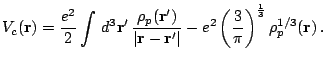 |
(26) |
The particle-particle (pairing) field is
![$\displaystyle \tilde U_q= \frac{t_0'}{2}(1-x_0')\tilde\rho_q +\frac{t_1'}{4}(1-...
...\Delta\tilde\rho_q\right] +\frac{t_3'}{12}(1-x_3')\rho^{\gamma'}\tilde\rho_q\,.$](img111.png) |
(27) |
Finally, the spin-orbit fields (
 )
have the following form factors:
)
have the following form factors:
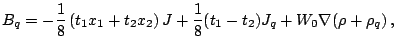 |
(28) |
![$\displaystyle \tilde B_q=\left[\frac{t_2'}{2}(1+x_2')+W_0'\right]\tilde J_q\,.$](img114.png) |
(29) |



Next: The Hartree-Fock-Bogolyubov equations
Up: The Skyrme Hartree-Fock-Bogolyubov equations
Previous: The Hartree-Fock-Bogolyubov energy
Jacek Dobaczewski
2005-01-23
![]() and
and
![]() to conserve the average neutron and proton number.
The HFB equations are then obtained by writing the stationary
condition
to conserve the average neutron and proton number.
The HFB equations are then obtained by writing the stationary
condition
![]() .
The dependence of
.
The dependence of
![]() on the kinetic densities leads
the effective mass
on the kinetic densities leads
the effective mass
![$\displaystyle \displaystyle \frac{\hbar^2}{2m}+\frac{t_1}{4}
\left[\left(1+\frac{x_1}{2}\right)\rho
-\left(x_1+\frac{1}{2}\right)\rho_q\right]\hfill$](img100.png)
![$\displaystyle \hskip 1.4cm +\frac{t_2}{4}\left[\left(1+\frac{x_2}{2}\right)\rho
+\left(x_1+\frac{1}{2}\right)\rho_q\right]$](img101.png)
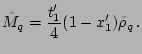
![$\displaystyle \displaystyle
t_0\left[\left(1+\frac{x_0}{2}\right)\rho
-\left(x_0+\frac{1}{2}\right)\rho_q\right] \hfill$](img104.png)
![$\displaystyle \displaystyle
\frac{t_1}{4}\left[\left(1+\frac{x_1}{2}\right)
\le...
..._1+\frac{1}{2}\right)\left(\tau_q-\frac{3}{2}\Delta\rho_q\right)
\right] \hfill$](img105.png)
![$\displaystyle \displaystyle
\frac{t_2}{4}\left[\left(1+\frac{x_2}{2}\right)
\le...
..._2+\frac{1}{2}\right)\left(\tau_q+\frac{1}{2}\Delta\rho_q\right)
\right] \hfill$](img106.png)
![$\displaystyle \displaystyle
\frac{t_3}{12}\left[\left(1+\frac{x_3}{2}\right)(2+...
...mma\rho^{\gamma-1}\sum_{q'}\rho_{q'}^2
+2\rho^\gamma\rho_q\right)\right] \hfill$](img107.png)


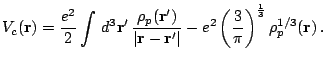
![$\displaystyle \tilde U_q= \frac{t_0'}{2}(1-x_0')\tilde\rho_q +\frac{t_1'}{4}(1-...
...\Delta\tilde\rho_q\right] +\frac{t_3'}{12}(1-x_3')\rho^{\gamma'}\tilde\rho_q\,.$](img111.png)
![$\displaystyle \tilde B_q=\left[\frac{t_2'}{2}(1+x_2')+W_0'\right]\tilde J_q\,.$](img114.png)