


Next: Numerical treatment of the
Up: Observables and single particle
Previous: Canonical basis
The rms radii for protons and neutrons are defined as
( or
or  )
)
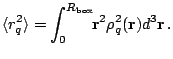 |
(55) |
The charge radius is obtained from the proton radius by taking into
account the proton charge distribution in an approximate way, i.e.,
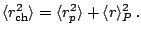 |
(56) |
with
 fm. The mean gaps are the average
values of the pairing fields
fm. The mean gaps are the average
values of the pairing fields
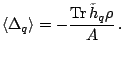 |
(57) |
The fluctuations of the particle numbers are defined as
 and
given by
and
given by
![$ 2\mathrm{Tr}\left[\rho_q^2-\rho_q\right]$](img211.png) .
.
Finally, the
rearrangement energy, which comes from the density dependence of
the force, and which shows how much the force is modified by the medium
effects, is given by



Next: Numerical treatment of the
Up: Observables and single particle
Previous: Canonical basis
Jacek Dobaczewski
2005-01-23
![]() or
or ![]() )
)
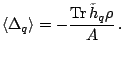
![$\displaystyle \displaystyle
\frac{t_3}{24}\gamma\rho^\gamma\left[\left(
1+\frac{x_3}{2}\right)\rho^2-\left(x_3+\frac{1}{2}\right)
\sum_q\rho_q^2\right]\hfill$](img213.png)
