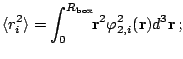Next: Canonical basis
Up: Observables and single particle
Previous: Observables and single particle
Hartree-Fock equivalent energies, radii, and nodes of
quasiparticle wave functions
For each quasiparticle state, in addition to its quasiparticle energy
 given by the HFB equation, one has several other
characteristics, which are defined
the following way:
given by the HFB equation, one has several other
characteristics, which are defined
the following way:
- the occupation factor
 which is the norm of the
lower component of the HFB quasiparticle wave function;
which is the norm of the
lower component of the HFB quasiparticle wave function;
- the (Hartree-Fock) equivalent energy
 which
is defined by applying the BCS type formula to the occupation factor
which
is defined by applying the BCS type formula to the occupation factor  , i.e.,
, i.e.,
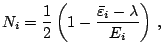 |
(45) |
which gives
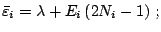 |
(46) |
- in the same spirit, the equivalent gap
 is defined by applying the BCS type formula to the
HFB quasiparticle energy
is defined by applying the BCS type formula to the
HFB quasiparticle energy  , i.e.,
, i.e.,
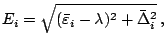 |
(47) |
which gives
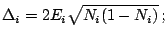 |
(48) |
- the rms radius
 is calculated using the lower
component of the quasiparticle wave function
is calculated using the lower
component of the quasiparticle wave function
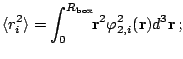 |
(49) |
- the number of nodes of the HFB quasiparticle wave function is defined
as the number of nodes (including the node at the origin but not
the one at infinity) of the component which has the greatest
amplitude.
These characteristics of the quasiparticle states can be found
in the output file hfb_n_p.spe, see Sec. 7.



Next: Canonical basis
Up: Observables and single particle
Previous: Observables and single particle
Jacek Dobaczewski
2005-01-23
![]() given by the HFB equation, one has several other
characteristics, which are defined
the following way:
given by the HFB equation, one has several other
characteristics, which are defined
the following way: