


Next: Continuity equation for the
Up: Continuity equation in the
Previous: Time evolution of a
Time-dependent density functional theory
In the framework of the time-dependent
Hartree-Fock (TDHF) approximation or time-dependent
density functional theory (TDDFT), the so-called
memory effects are often neglected and it is assumed that the potential at
time  is just the static potential evaluated at the
instantaneous density [G. F. Giuliani and G. Vignale,The Quantum Theory Of The Electron Liquid, (Cambridge University Press, Cambridge, 2005)()]. For these two time-dependent
approaches, the starting point is the equation of motion
for the one-body density matrix
is just the static potential evaluated at the
instantaneous density [G. F. Giuliani and G. Vignale,The Quantum Theory Of The Electron Liquid, (Cambridge University Press, Cambridge, 2005)()]. For these two time-dependent
approaches, the starting point is the equation of motion
for the one-body density matrix
 [14,13],
[14,13],
![\begin{displaymath}
i\hbar \frac{{\rm d}}{{\rm d} t}\rho = [h,\rho]
,
\end{displaymath}](img41.png) |
(9) |
where the mean-field Hamiltonian
 is defined as the derivative
of the total energy
is defined as the derivative
of the total energy  with respect to the density matrix,
with respect to the density matrix,
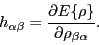 |
(10) |
In the present study we are concerned with the Kohn-Sham approach [15],
whereby the total energy is the sum of the kinetic and potential-energy terms,
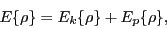 |
(11) |
where
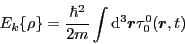 |
(12) |
and
 is the scalar-isoscalar kinetic density, see, e.g., Ref. [16]
for definitions. The nonlocal density,
can be defined in terms of either the fixed-basis orbitals,
is the scalar-isoscalar kinetic density, see, e.g., Ref. [16]
for definitions. The nonlocal density,
can be defined in terms of either the fixed-basis orbitals,
 ,
,
or instantaneous Kohn-Sham orbitals,
 ,
,
The mean-field Hamiltonian
is the sum of kinetic and potential-energy terms,
 , where
, where
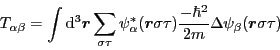 |
(15) |
and
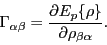 |
(16) |
Let us now assume that the potential energy is invariant with respect
to a unitary transformation of the density matrix [14,13],
 , that is,
for all parameters
, that is,
for all parameters  we have,
we have,
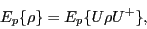 |
(17) |
where
 is the hermitian matrix of a one-body symmetry generator.
Then, the first-order expansion in
is the hermitian matrix of a one-body symmetry generator.
Then, the first-order expansion in  ,
,
![\begin{displaymath}
E_p \{U\rho U^+\} \simeq E_p \{\rho\}
+\eta \sum_{\beta\alp...
...al (U\rho U^+)_{\beta\alpha}}{\partial \eta}\right]_{\eta=0}
,
\end{displaymath}](img60.png) |
(18) |
gives a condition for the energy to be invariant with respect to this unitary transformation, that is
![\begin{displaymath}
\mbox{Tr}\Gamma[G,\rho] \equiv \mbox{Tr}G[\Gamma,\rho] = 0
,
\end{displaymath}](img61.png) |
(19) |
which allows us to derive the equation of motion for the average value
of
 . Indeed, from the TDDFT equation (9)
we then have:
. Indeed, from the TDDFT equation (9)
we then have:
![\begin{displaymath}
i\hbar \frac{{\rm d}}{{\rm d} t}\langle G\rangle
= i\hbar \m...
...d}}{{\rm d} t}\rho = \mbox{Tr}G[h,\rho] = \mbox{Tr}G[T,\rho]
,
\end{displaymath}](img63.png) |
(20) |
that is, the time evolution of
 is governed solely
by the kinetic term of the mean-field Hamiltonian.
is governed solely
by the kinetic term of the mean-field Hamiltonian.
Subsections



Next: Continuity equation for the
Up: Continuity equation in the
Previous: Time evolution of a
Jacek Dobaczewski
2011-11-11
![]() is just the static potential evaluated at the
instantaneous density [G. F. Giuliani and G. Vignale,The Quantum Theory Of The Electron Liquid, (Cambridge University Press, Cambridge, 2005)()]. For these two time-dependent
approaches, the starting point is the equation of motion
for the one-body density matrix
is just the static potential evaluated at the
instantaneous density [G. F. Giuliani and G. Vignale,The Quantum Theory Of The Electron Liquid, (Cambridge University Press, Cambridge, 2005)()]. For these two time-dependent
approaches, the starting point is the equation of motion
for the one-body density matrix
![]() [14,13],
[14,13],
![]() , that is,
for all parameters
, that is,
for all parameters ![]() we have,
we have,