Description of pairing correlations

In our SHF+BCS approach, we use the Skyrme energy density functional in its SLy4 parameterization[11] in the particle-hole channel, whereas two different pairing schemes were implemented in the particle-particle channel. The SHF+BCS(G) scheme employs the seniority pairing force with strength parameters defined as in Ref.[12], i.e.,

$$\begin{array}{l} G^{n}=\left[19.3-0.084 \left( N-Z \right)\r... ...=\left[13.3+0.217 \left( N-Z \right)\right]/A\,,\\ \end{array}$$ (1)

additionally scaled by

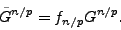$$\tilde{G}^{n/p}= f_{n/p}G^{n/p}.$$ (2)

In the SHF+BCS($\delta$) scheme, we apply the state-dependent $\delta$-interaction[13] with commonly used parameterization variants,[14] which are summarized as

$$\begin{array}{rcl} V^{n/p}_{\delta}\left(\vec{r}_{1},\vec{r}... ...\right] \delta\left(\vec{r}_{1}-\vec{r}_{2}\right), \end{array}$$ (3)

where $\rho_{0}=0.16\,\mbox{fm}^{-3}$ and

$$\begin{array}{rcl} \eta&=&\left\{ \begin{array}{ll} 0\,, & ... ...textit{surface} pairing (MIX).} \end{array}\right. \end{array}$$ (4)

The scaling factors of Eq. (2), $f_{n}=1.41$ and $f_{p}=1.13$, and pairing strengths $V^{n}_{0}=282.0$ MeV, $V^{p}_{0}=285.0$ MeV (DI), $V^{n}_{0}=842.0$ MeV, $V^{p}_{0}=1020.0$ MeV (DDDI), and $V^{n}_{0}=425.5$ MeV, $V^{p}_{0}=448.5$ MeV (MIX) were adjusted to reproduce the experimental[15] neutron ( $\Delta_{n}=0.696$ MeV) and proton ( $\Delta_{p}=0.803$ MeV) pairing gaps in $^{252}$Fm. As we deal with contact interactions, we use a finite pairing-active space defined by including $\Omega^{n/p}=(N \mbox{ or } Z)$ lowest single-particle states for neutrons and protons, respectively. In the SHF+BCS($\delta$) approach, the pairing gap is state dependent. Therefore, the average (spectral) gaps,

$$\langle\Delta_{n/p}\rangle = \frac{\sum_{k\in \Omega^{n/p}} v_{k} u_{k}\Delta_{k}} {\sum_{k\in \Omega^{n/p}} v_{k}u_{k}}\,,$$ (5)

were used as measures of experimental pairing gaps deduced from the odd-even mass staggering. In Eq. (5) $v_{k}$ and $u_{k}$ are the BCS occupation amplitudes (see, e.g., Ref.[16] for a more detailed discussion).

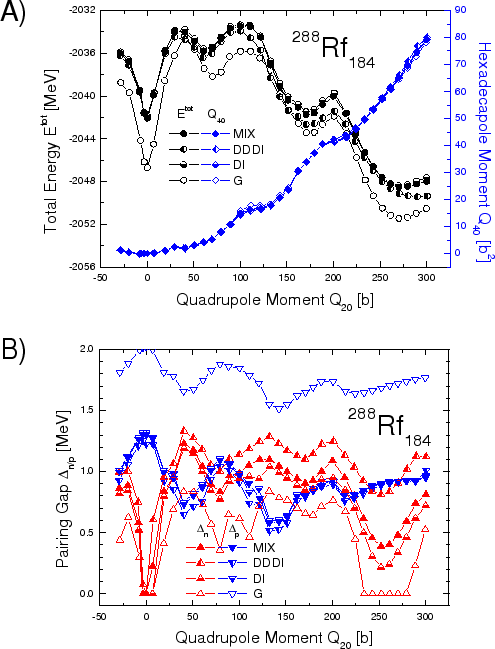
Figure: (A) The total binding energies $E^{\mbox{\scriptsize{tot}}}$ (left-hand side scale) and mass hexadecapole moments $Q_{40}$ (right-hand side scale) along the fission paths of $^{288}$Rf$_{184}$ calculated with the SLy4 interaction and four different pairing interactions: MIX, DDDI, and DI $\delta$-interaction, and seniority pairing (G). (B) The neutron $\Delta _{n}$ and proton $\Delta _{p}$ pairing gaps along the fission paths shown above.

The calculations were carried out using the code HFODD (v.2.19l)[17,18,19] that solves self-consistent HF equations by using a Cartesian 3D deformed harmonic-oscillator finite basis. In the calculations, we took the lowest 1140 single-particle states for the basis. This corresponds to 17 oscillator shells at the spherical limit.