


Next: Results
Up: Approximations to ATDHFB
Previous: Gaussian overlap approximation
Treatment of proton and neutron contributions
The above expressions for the mass tensor are valid for one kind of
fermions only. In the case of the cranking approximation, the total mass
tensor is a sum of neutron and proton contributions:
 |
(65) |
In the GOA, however, the total inverse inertia
 for a
composite system is given as a sum of proton and neutron inverse covariant
inertia tensors [24]:
for a
composite system is given as a sum of proton and neutron inverse covariant
inertia tensors [24]:
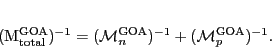 |
(66) |
Jacek Dobaczewski
2010-07-28