Local energy density for spinless particles of one kind

In this section, we consider the simplest (and academic) case of fermions with no spin and no isospin. First we recall that for an arbitrary non-local finite-range interaction $V(\mbox{{\boldmath {$r$}}}'_1,\mbox{{\boldmath {$r$}}}'_2;\bboxr_1,\bboxr_2)$, the Kohn-Sham interaction energy [21] has the form

$${\cal E}^{\text{int}} = {\textstyle{\frac{1}{2}}}\int{\rm d}^3\mbox{{\boldmath {$r$}}}'_1... ...{\boldmath {$r$}}}'_1, \mbox{{\boldmath {$r$}}}'_2; \bboxr_1, \bboxr_2) \times$$

$$~~~~~~~~~~~~ \big(\rho(\bboxr_1,\mbox{{\boldmath {$r$}}}'_1)\rho... ...2,\mbox{{\boldmath {$r$}}}'_1)\rho(\bboxr_1,\mbox{{\boldmath {$r$}}}'_2)\big) ,$$ (1)

whereas for a local interaction,

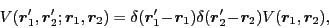$$V(\mbox{{\boldmath {$r$}}}'_1,\mbox{{\boldmath {$r$}}}'_2;\... ...x{{\boldmath {$r$}}}'_2\!-\!\bboxr_2) V(\bboxr_1,\bboxr_2) ,$$ (2)

the interaction energy reduces to:

$${\cal E}^{\text{int}} = {\textstyle{\frac{1}{2}}}\int{\rm d}^3\bboxr_1{\rm d}^3\bboxr_2 ... ...\bboxr_1)\rho(\bboxr_2) - \rho(\bboxr_2,\bboxr_1)\rho(\bboxr_1,\bboxr_2)\Big),$$ (3)

where $\rho(\bboxr_1)\equiv\rho(\bboxr_1,\bboxr_1)$ and $\rho(\bboxr_2)\equiv\rho(\bboxr_2,\bboxr_2)$ are local densities. As is well known, the first term in Eq. (3) (the direct term) depends only on local densities, whereas the second one (the exchange term) depends on the modulus squared of the non-local density. This markedly different structure of the two terms requires separate treatment, as discussed in the following two subsections.