


Next: Fitting procedure
Up: Shell-structure fingerprints of tensor
Previous: Introduction
Tensor and spin-orbit parts of the local nuclear
energy density functional
In this work we consider the local EDF,
 , of the Skyrme-type.
It consists of a kinetic energy and a sum of isoscalar (
, of the Skyrme-type.
It consists of a kinetic energy and a sum of isoscalar ( =0) and isovector
(
=0) and isovector
( =1) potential energy terms:
=1) potential energy terms:
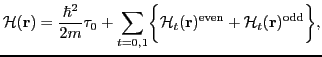 |
(1) |
where
with the density-dependent primary coupling constants
![$ C^{\rho}_t[\rho_0]$](img30.png) and
and
![$ C^{s}_t [\rho_0 ]$](img31.png) . The potential energy terms are bilinear forms of
either time-even (
. The potential energy terms are bilinear forms of
either time-even ( ,
,  ,
,
 )
or time-odd (
)
or time-odd (
 ,
,
 ,
,
 ) densities
and their derivatives, see, e.g., Ref. [10] for details.
The
) densities
and their derivatives, see, e.g., Ref. [10] for details.
The
 density denotes the vector part of the spin-current
tensor,
density denotes the vector part of the spin-current
tensor,
 .
.
In this work we focus on the tensor,
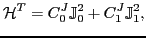 |
(4) |
and the SO terms,
 |
(5) |
In the limit of spherical symmetry, the vector
part
 is the only
non-vanishing part of the tensor density
is the only
non-vanishing part of the tensor density
 .
Hence, in this limit, the tensor part of the functional (4)
reduces to:
.
Hence, in this limit, the tensor part of the functional (4)
reduces to:
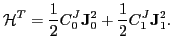 |
(6) |
By performing variation of the functional with respect
to  one obtains the one-body SO potential:
one obtains the one-body SO potential:
which is composed of two terms. The first term is
coming form the SO term in the functional, Eq. (5). It is proportional
to the radial derivative of the particle density and is relatively
slowly varying with  and
and  . The second component is due to the
tensor term (4). It is proportional to the SO density
. The second component is due to the
tensor term (4). It is proportional to the SO density  which
is strongly shell-filling dependent. Indeed,
in the spherical symmetry limit, the SO vector
density can be written as [26]:
which
is strongly shell-filling dependent. Indeed,
in the spherical symmetry limit, the SO vector
density can be written as [26]:
where  and
and
 are occupation probabilities and
radial wave functions, respectively, of states with given quantum numbers.
If both SO partners
are occupation probabilities and
radial wave functions, respectively, of states with given quantum numbers.
If both SO partners
 are fully occupied,
i.e., when the system is spin-saturated (SS) the
are fully occupied,
i.e., when the system is spin-saturated (SS) the  density vanishes.
Examples of the SS systems include
density vanishes.
Examples of the SS systems include  O,
O,
 Ca, or
Ca, or  Zr at spherical shape. Most of the nuclei are
spin-unsaturated (SUS). The SO vector density reaches its maximum when one
(or more) of the SO partners is fully occupied while the other one is
completely empty.
Zr at spherical shape. Most of the nuclei are
spin-unsaturated (SUS). The SO vector density reaches its maximum when one
(or more) of the SO partners is fully occupied while the other one is
completely empty.



Next: Fitting procedure
Up: Shell-structure fingerprints of tensor
Previous: Introduction
Jacek Dobaczewski
2009-04-13
![]() , of the Skyrme-type.
It consists of a kinetic energy and a sum of isoscalar (
, of the Skyrme-type.
It consists of a kinetic energy and a sum of isoscalar (![]() =0) and isovector
(
=0) and isovector
(![]() =1) potential energy terms:
=1) potential energy terms: