Wnioskowanie Statystyczne

1. Znajdźmy prawdopodobieństwo, że Z < −2,47. Proszę zrobić to na dwa sposoby: raz z użyciem wygenerowanych zmiennych z rozkładu normalnego, drugi raz z użyciem dystrybuanty norm.cdf.
[Odp: p = 0,0068]

import scipy.stats as st

N = 100000
z_crit = -2.47
Z = st.norm.rvs(loc=0, scale=1, size=N)
p = sum(Z < z_crit)/N
p_cdf = st.norm.cdf(z_crit, loc=0, scale=1)

print('symulowane p: %.4f' % p )
print('p z dystrybuanty: %.4f' % p_cdf)



2. Znaleźć prawdopodobieństwo P(|Z| < 2)

[Odp: p = 0,9545]
import scipy.stats as st
import numpy as np

N = 100000
z_crit = 2
Z = st.norm.rvs(loc=0, scale=1, size=N)
p = sum(np.abs(Z) < z_crit)/N
p_cdf = st.norm.cdf( z_crit, loc=0, scale=1) - st.norm.cdf( -z_crit, loc=0, scale=1)

print('symulowane p: %.4f' % p )
print('p z dystrybuanty: %.4f' % p_cdf)

3. Koncentracja zanieczyszczeń w półprzewodniku używanym do produkcji procesorów podlega rozkładowi normalnemu o średniej 127 cząsteczek na milion i odchyleniu standardowemu 22. Półprzewodnik może zostać użyty jedynie gdy koncentracja zanieczyszczeń spada poniżej 150 cząstek na milion. Jaka proporcja półprzewodników nadaje się do użycia?
Prawdopodobieństwo obliczyć korzystając z dystrybuanty rozkładu normalnego oraz z symulacji.
 [Odp: p = 0,852]
import scipy.stats as st
import pylab as py
import numpy as np

mu = 127
sig = 22
m_kryt = 150

#wzór
p = st.norm.cdf(m_kryt, loc = mu, scale = sig )
print('proporcja odczytana z dystrybuanty rozkładu normalnego: %4g' %p)

# symulacja
N_pro b= 10000
seria = st.norm.rvs(loc=mu, scale=sig, size=N_prob)
p = sum(seria<=m_kryt)/N_prob
bins = np.arange(60,200,5)
h = py.hist(seria,bins);
py.plot([m_kryt, m_kryt],[0, max(h[0])],'r')
p1 = np.sum(seria<=m_kryt)/N_prob

print('prawdopodobieństwo uzyskane z symulacji: %.4g' %p1)
py.show()

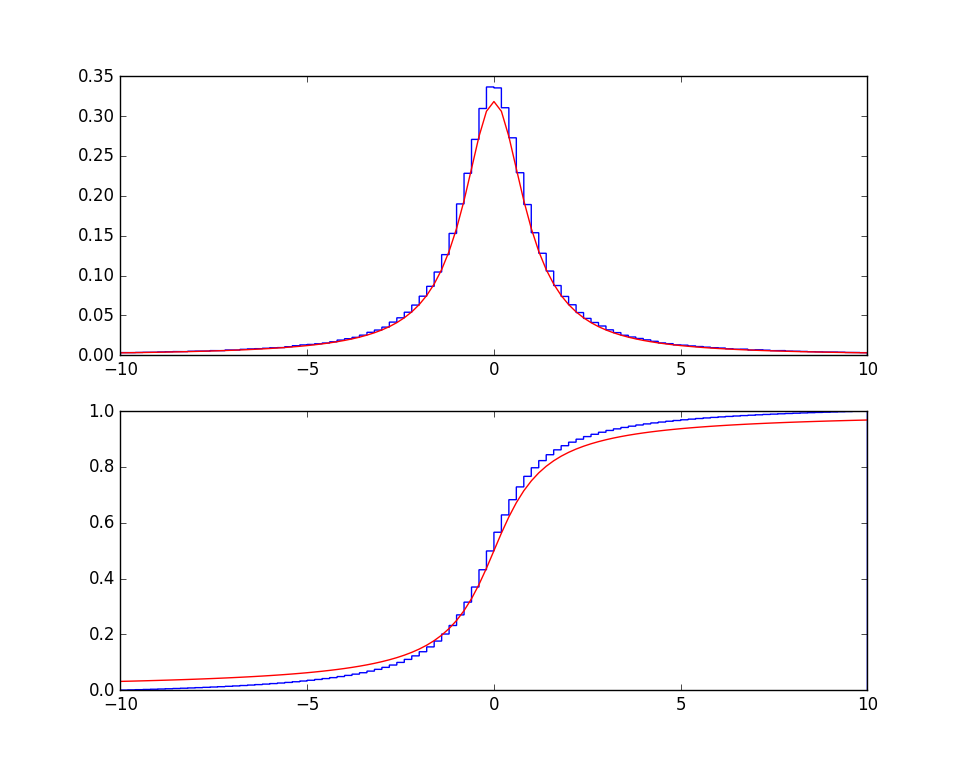
4. Posiłkując się  przykładem napisz funkcję MyGen(N) dla rozkładu, którego funkcja gęstości prawdopodobieństwa jest dana wzorem: $$f(x) = \frac{1}{\pi (1+x^{2})}.$$ Następnie narysuj dla niego dystrybuantę i dystrybuantę empiryczną na przedziale [-10, 10].

import scipy.stats as st
import numpy as np
import matplotlib.pyplot as plt

def f_odwrotna(N):
    y = np.random.random(N)
    return np.tan(np.pi*(y - 0.5))

def dystrybuanta(X, od=-10, do=10, krok=0.1):
    os_x = np.arange(od, do, krok)
    nx = len(os_x)
    N_liczb = len(X)
    D = np.zeros(nx)
    for i in range(nx):
        D[i] = sum(X <= os_x[i])/N_liczb
    return (os_x, D)

N = 10000
x = np.arange(-10, 10, 0.1)
F = np.arctan(x)/np.pi + 0.5
X = f_odwrotna(N)
(os_x, F_emp) = dystrybuanta(X, od=-10, do=10, krok=0.1)
plt.plot(x, F, 'r', label='dystrybuanta teoretyczna')
plt.plot(os_x, F_emp, '.b', label='dystrybuanta empiryczna')
plt.legend()
plt.show()