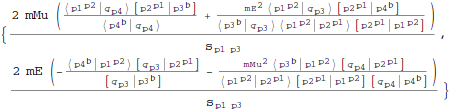QED with muons
In this tutorial we illustrate how the SpinorsExtras package can be used for calculation of amplitudes including massive spinors and vector bosons on the simple case of QED with photons, electrons and muons. As an example, we calculate the tree level amplitude for
e- -→e-
-→e- -
- scattering using on-shell recursion method. Than we compare it with amplitude calculated using Feynman diagrams and test invariance with respect to change of various reference vectors.
Throughout this tutorial basic familiarity with S@M package is assumed and only functions added in SpinorsExtras package are introduced in definition boxes.
To use SpinorsExtras, one needs to import the package first:
On-shell recursion
| SpM[p,1] | Labels u spinor for massive momentum p. |
PolVec[k,pol] or 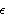 pol(k) pol(k) | Labels polarization vector for momentum k, and polarization pol. |
| LightConeDecompose[expr,patt] | Performs light cone decomposition of those massive Lorentz vectors and spinors, in expr, that match patt. |
| SpRef[k] or qk | Labels default reference spinor for Lorentz vector k. |
| SpAssoc[p,q] or pq | Labels vector associated with massive momentum p by light cone decomposition with (massive or massless) reference vector q. |
| ExpandPolVec[expr] | Expresses polarization vectors in expr by momentum and reference vectors. |
| ReplaceLVector[expr,x→y] | Replaces, in expr, Lorentz vectors labeled by x with Lorentz vectors labeled by y. |
| ReplaceSpinor[expr, x→y] | Replaces, in expr, spinors labeled by x with spinors labeled by y. |
| ExplicitRef[expr,patt] | Adds explicit reference vectors to all massive spinors, in expr, that match patt. |
| ShiftBA[p1,p2,z][expr] | For massive Lorentz vectors p1, p2, performes shift described in |
| RefSimplify[expr,patt] | Finds simplest form of expr with respect to change of reference vectors matching patt. |
Functions used to calculate amplitudes using on-shell recursion.
We start from performing the amplitude calculation using the on-shell recursion technique. It can be done with following steps:
Define basic fermion-vector boson-fermion three point amplitudes:
Declare symbol to be treated as massless labels (
k and
mk will denote momentum of on-shell photon):
Declare symbols to be treated as massive labels (
p1,
p3 will denote on-shell momenta of massive electrons;
p2,
p4 momenta of muons;
kOff will denote momentum of off-shell photon):
Calculate electron muon scattering diagrams with on-shell photon 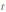 -channel exchange. Electrons have positive and muons negative spin projections. Diagram consists of two fermion-vector boson-fermion three point amplitudes connected by photon line. Momentum transfer is denoted by k. Symbols from S@M package are linear in labels. We a priori don't know whether label representing four-momentum -k will appear in place where it'll be interpreted as object scaling linearly with four-momentum, or as object scaling as square root of four-momentum. In first case it should be labeled by -k and in latter case by ± I k, so we temporarily use mk to represent it.
| Out[10]= |  |
|
Decompose spinors for "final" particles:
| Out[11]= | 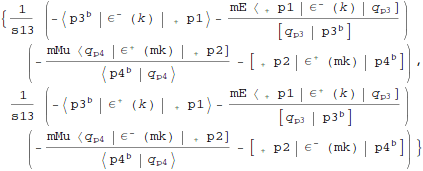 |
Express polarization vectors by momentum and reference vectors:
| Out[12]= | 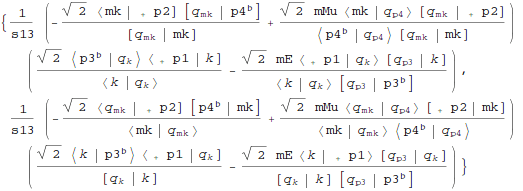 |
Lorentz vectors labeled by
mk can now be replaced with
-k and spinors labeled by
mk can be replaced with ±
I k (in this simple example there are actually no Lorentz vectors
mk only spinors):
| Out[14]= | 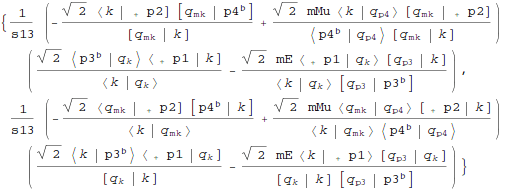 |
Add explicit reference vectors to massive spinors that we intend to shift:
| Out[15]= | 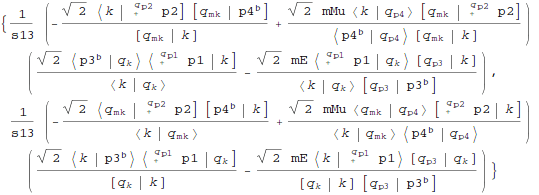 |
Replace default reference vectors with reference vectors for which boundary term, for further shift, will vanish:
| Out[16]= | 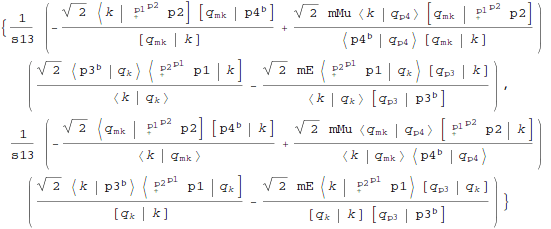 |
Find
z that will put shifted momentum transfer on-shell:
| Out[17]= | 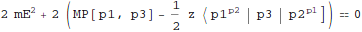 |
| Out[18]= | 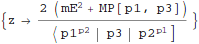 |
Perform holomorphic shift of
p1 and
p2 in diagrams (in this simplified example there is actually nothing to shift except momentum transfer which we'll consider separately) and insert proper
z:
| Out[19]= | 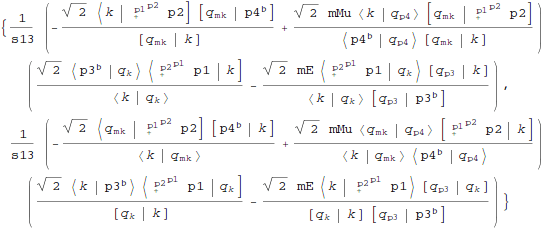 |
After shift we can decompose remaining massive spinors:
| Out[21]= | 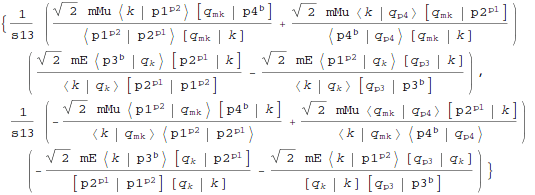 |
Spinors related to shifted, on-shell momentum transfer are proportional to slashed off-shell momentum transfer acting on proper spinors related to complexification vector (normalization factor can be added to any spinor):
| Out[22]= | 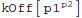 |
| Out[23]= |  |
Express photons momentum by external momenta:
| Out[27]= | 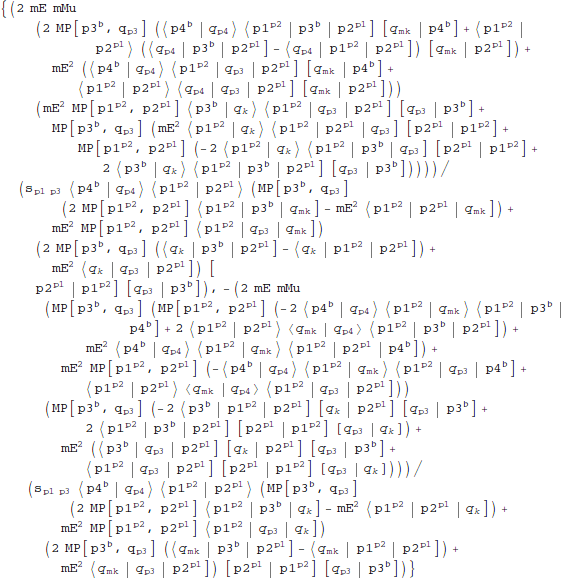 |
Find simplest form of diagrams with respect to reference vectors of exchanged photon (this may take some time).
Note that since each diagram is gauge invariant we can simplify diagrams separately, so we map
RefSimplify on list of diagrams:
| Out[28]= | 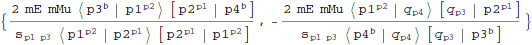 |
| Out[29]= |  |
Numerical results and comparison with standard amplitude
As we illustrate below SpinorsExtras package can be also used to calculate numerical values of scattering amplitudes. They can be used e.g. for testing the final result by comparing it with amplitude obtained using ordinary Feynman diagrams.
Assign numerical values to masses
:Generate random numerical momenta for external particles (such that
p1+p2=p3+p4)
:Assign default numerical values to reference vectors for "final" particles
:Assign numerical values to associated vectors
:Comparison with standard amplitude
Calculate electron muon scattering amplitude using ordinary Feynman diagrams (there is just one diagram: with off-shell photon
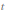
-channel exchange):
| Out[40]= | 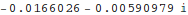 |
Compute numerical value of amplitude calculated using on-shell recursion and compare it with amplitude calculated using Feynman diagrams:
| Out[41]= | 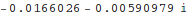 |
| Out[42]= | 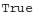 |
Reference vectors independence
Functions used to test numerical invariance of amplitude.
Independence of the final results on the choice of reference vectors can be used as additional test of the correctness of the final result:
Assign random numerical values to reference vectors for exchanged photon
:Set accuracy of numerical invariance tests
:Test invariance of diagrams with respect to change of reference vectors of on-shell photon
:
| Out[45]= | 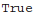 |
| Out[46]= | 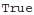 |
Test invariance of amplitude with respect to change of reference vectors of external final particles (since different reference vectors correspond to different, distinguishable states, amplitude is not invariant). Invariance testing function needs to take into account all occurrences of reference vector, so we make all occurrences explicit
.
| Out[47]= | 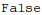 |
| Out[48]= | 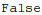 |
Calculate amplitudes with changed spin projections of final particles
:
| Out[68]= | 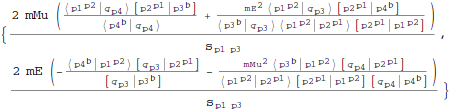 |
Square of absolute value of amplitude summed over spin projections of given particle should be independent of reference vector related to this particle
:
| Out[69]= | 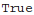 |
| Out[70]= | 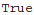 |
 -→e-
-→e- - scattering using on-shell recursion method. Than we compare it with amplitude calculated using Feynman diagrams and test invariance with respect to change of various reference vectors.
- scattering using on-shell recursion method. Than we compare it with amplitude calculated using Feynman diagrams and test invariance with respect to change of various reference vectors.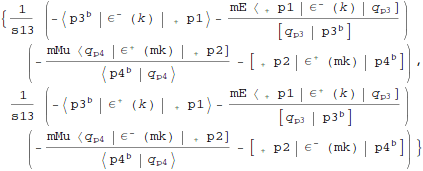
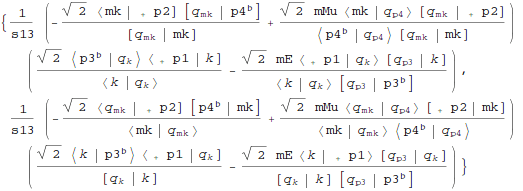
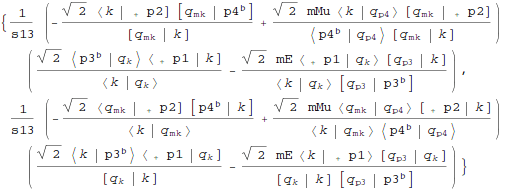
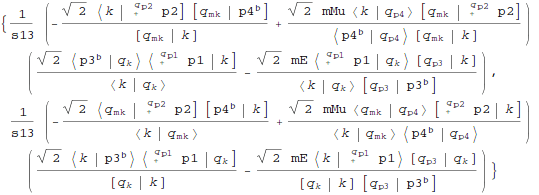
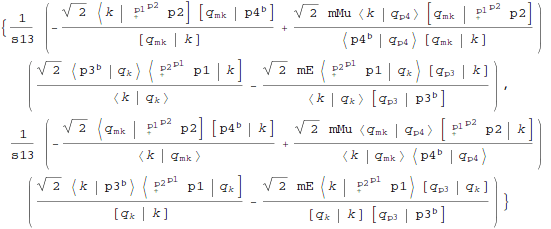
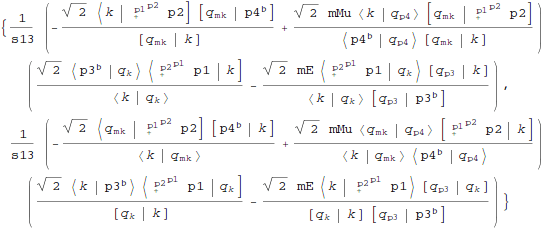
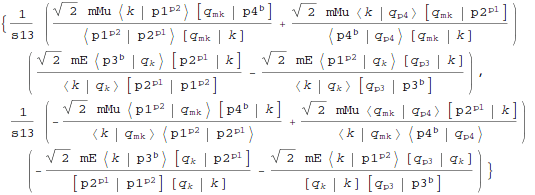
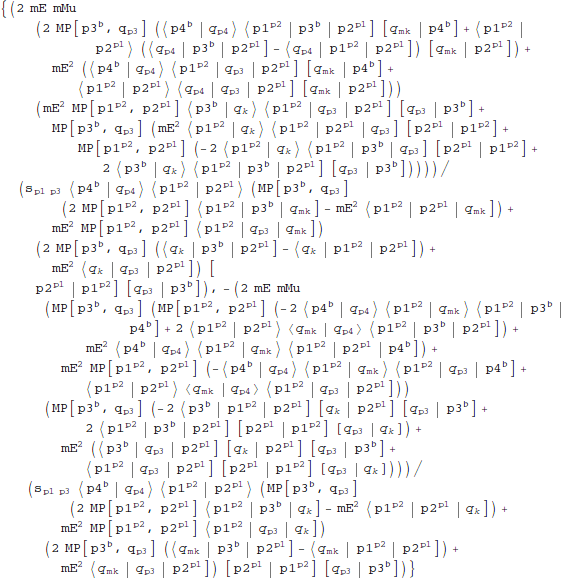

 -channel exchange):
-channel exchange):