SEARCH FOR FINGERPRINTS OF TETRAHEDRAL SYMMETRY IN $^{156}$Gd ¹

Q.T. Doan$^{1}$, D. Curien$^{2}$, O. Stézowski$^{1}$, J. Dudek$^{2}$, K. Mazurek$^{5}$, A. Gózdz$^{3}$, J. Piot$^{2}$, G. Duchêne$^{2}$, B. Gall$^{2}$, H. Molique$^{2}$, M. Richet$^{2}$, P. Medina$^{2}$,D. Guinet$^{1}$, N. Redon$^{1}$, Ch. Schmitt$^{1}$, P. Jones$^{4}$, P. Peura$^{4}$, S. Ketelhut$^{4}$, M. Nyman$^{4}$, U. Jakobsson$^{4}$, P.T. Greenlees$^{4}$, R. Julin$^{4}$, S. Juutinen$^{4}$, P. Rahkila$^{4}$, A. Maj$^{5}$, K. Zuber$^{5}$, P. Bednarczyk$^{5}$, N. Schunck$^{6}$, J. Dobaczewski$^{4,7}$, A. Astier$^{8}$, I. Deloncle$^{8}$, D. Verney$^{9}$, G. de Angelis$^{10}$ and J. Gerl$^{11}$

Abstract:

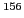
Theoretical predictions suggest the presence of tetrahedral symmetry as an explanation for the vanishing intra-band E2 transitions at the bottom of the odd-spin negative-parity band in $^{156}$Gd. The present study reports on experiment performed to address this phenomenon. 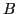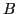It allowed to remove certain ambiguouities related to the intra-band E2 transitions in the negative-parity bands, to determine the new inter-band transitions and branching ratios $B$(E2)/$B$(E1) and, for the first time, to determine the exerimental uncertainties related to latter obervable.